LSCGAT: LONG SEQUENCES CUSTOMIZABLE GLOBAL ALIGNMENT TOOL
DOI: https://doi.org/10.18454/jbg.2019.1.10.1
Pankratov A.N. *1, Tetuev R.K. 2 , Pyatkov M.I. 3
1,2,3 Institute of Mathematical Problems of Biology RAS - the Branch of Keldysh Institute of Applied Mathematics of Russian Academy of Sciences, Pushchino, Russia
1 Pushchino State Institute of Natural Science, Pushchino, Russia
* Corresponding author (pan[at]impb.ru)
Received: 01.07.2019; Accepted: 08.07.2019; Published: 09.07.2019
LSCGAT: LONG SEQUENCES CUSTOMIZABLE GLOBAL ALIGNMENT TOOL
Application notes
Abstract
The most general model of a pairwise global alignment with the possibility of aligning long sequences is considered. The model features are alignment of sequences in different alphabets including nucleotides and amino acids, alternative alignments with the same score, predefined or fully customazible scoring matrix and gap penalty systems for each sequence including end gap penalties. Developed versatile parallel algorithm for global alignment is based on the Needleman-Wunsch algorithm with an arbitrary scoring matrix and Gotoh algorithm for the affine system of penalties for gaps. The main features of the algorithm include optimal memory consumption and parallel computation. It is proved that algorithm can align two sequences of length 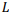 in memory space
in memory space 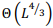 . The algorithm is implemented in the form of a high-performance web application in Javascript programming language with the usage of webworkers and is freely available on http://sbars.impb.ru/aligner.html.
. The algorithm is implemented in the form of a high-performance web application in Javascript programming language with the usage of webworkers and is freely available on http://sbars.impb.ru/aligner.html.
Keywords: scoring matrix, gap penalty, alternative alignment, long sequences.
Панкратов А.Н.*1 , Тетуев Р.К. 2 , Пятков М.И. 3
1,2,3 Институт математических проблем биологии РАН – филиал Института прикладной математики им. М.В. Келдыша РАН, Пущино, Россия
1 Пущинский государственный естественно-научный институт, Пущино, Россия
* Корреспондирующий автор (pan[at]impb.ru)
Получена: 01.07.201; Доработана: 08.07.2019; Опубликована: 09.07.2019
LSCGAT: ИНСТРУМЕНТ НАСТРАИВАЕМОГО ГЛОБАЛЬНОГО ВЫРАВНИВАНИЯ ДЛИННЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Техническая спецификация
Аннотация
Рассмотрена наиболее общая модель попарного глобального выравнивания с возможностью выравнивания длинных последовательностей. Особенности модели: выравнивание последовательностей в разных алфавитах, включая нуклеотиды и аминокислоты, альтернативные выравнивания с одинаковым счетом, предварительно заданные или полностью настраиваемые матрица замен и системы штрафов за пропуски для каждой последовательности, включая штрафы за концевые вставки. Разработанный универсальный параллельный алгоритм глобального выравнивания основан на алгоритме Нидлмана-Вунша с произвольной матрицей скоринга и алгоритме Гота для аффинной системы штрафов за пропуски. Основные характеристики алгоритма включают оптимальное потребление памяти и параллельные вычисления. Доказано, что алгоритм может выровнять две последовательности длины 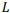 в пространстве памяти
в пространстве памяти 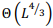 . Алгоритм реализован в виде высокопроизводительного веб-приложения на языке программирования Javascript с использованием фоновых веб-процессов и находится в свободном доступе по адресу http://sbars.impb.ru/aligner.html.
. Алгоритм реализован в виде высокопроизводительного веб-приложения на языке программирования Javascript с использованием фоновых веб-процессов и находится в свободном доступе по адресу http://sbars.impb.ru/aligner.html.
Ключевые слова: матрица замен, штрафы за пропуски, альтернативные выравнивания, длинные последовательности.
1. Introduction
In this paper, we consider the classical algorithm of bioinformatics - the Needleman-Wunsch algorithm [1] for the global alignment of nucleotide and amino acid sequences. The aim of this work is to develop a tool for assessing the similarity of extended repeats in genomes which can be detected by the generalized spectral-analytical method [2]. Modern implementations of the global alignment algorithm such as corresponding services of NCBI BLAST and EMBOSS take into account the affine penalties system for insertions proposed in the work [3], as well as the penalty system for insertions at the ends of sequences. At the same time, the parameters of the method in these implementations cannot always be changed within the desired limits, and the questions of choosing a unique alignment from a variety of alternative solutions are solved in different ways. Thus, each implementation has its own characteristics which do not allow to compare it exactly with others. Moreover, the main limitation of these realizations is the length of the studied sequences being, as a rule, tens of thousands of nucleotides. This is due to the fact that the algorithm of global alignment is quadratic in both memory and speed, depending on the length of the processed sequences. Overcoming the memory complexity of the algorithm was made in the work [4], which proposed lowering the memory consumption to linear due to the recursive approach. The essence of this approach is that one of the sequences is divided in half and there is a corresponding point in the second sequence through which the optimal alignment passes. After that, the task is recursively reduced to aligning two pairs of fragments, etc. At the same time, the theoretical computational complexity is doubled in comparison with the classical algorithm in which the scoring matrix is stored in memory. In this paper, the grid scheme of the algorithm, proposed in the work [5], is taken as a basis which allows both saving memory and parallelizing computations. In the grid scheme, the score matrix is divided into blocks, the memory is allocated to the values of the matrix elements at the block boundaries, and the values of the matrix elements inside the blocks can be calculated starting from the boundary ones. Calculations are saved by the fact that on the back pass of dynamic programming a small number of blocks are subject to recovery. It is shown that in the case of recursive application this approach also reduces the use of memory to linear. However, unlike the works of [4,5] which proposed algorithms with linear memory growth, in this work the minimum of required memory is obtained as the balance between its use in the forward and reverse pass of the method without recursion. It is shown that, although memory growth in this case is greater than linear memory, it allows aligning sequences up to a million nucleotides. At the same time, the developed algorithm is characterized by a good scalability of computations on multi-core computing systems [6,7].
2. Methods
Suppose that L1( and L2) are the lengths of the sequences being compared, H1( and H2) are the grid steps for each sequence, respectively. Evaluation of the memory used by the algorithm contains two terms, the amount of memory on the forward and backward pass:
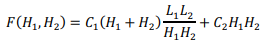
The first term is obtained by multiplying the number of blocks of the grid 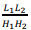 by the number of stored boundary elements of each block
by the number of stored boundary elements of each block 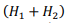 with the constant C1, which determines the amount of memory for one element of the matrix. The second term is proportional to the number of elements of one matrix block H1(H2) with the constant C2.
with the constant C1, which determines the amount of memory for one element of the matrix. The second term is proportional to the number of elements of one matrix block H1(H2) with the constant C2.
Constants in the current implementation are selected as follows: 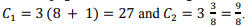 .
.
On the forward pass the score value is encoded by 8 bytes. Additionally, one byte reserved for a vector of backward path which is encoded by 3 bits. It is multiplied by 3, the number of variants of scores and paths for the affine penalty system. On the return pass, when the matrix is reconstructed inside the block, only a vector of paths has to be stored because there is no need to store scores for internal elements. Additionally, in the current version, paths vectors are packed into the array of memory allocated for the matrix.
The minimum value of the memory expression is equal
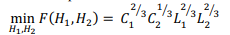
and is achieved at: 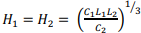 . Note that even in the case of a rectangular matrix
. Note that even in the case of a rectangular matrix 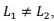 the optimal size of the grid block is obtained to be the square
the optimal size of the grid block is obtained to be the square 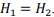 That is because the amount of memory used is proportional to the perimeter of the block. The optimal shape of the block is a square which contains the maximal number of elements with a minimal perimeter.
That is because the amount of memory used is proportional to the perimeter of the block. The optimal shape of the block is a square which contains the maximal number of elements with a minimal perimeter.
3. Results
The program has the following options: an arbitrary scoring matrix, switching between three classic models of penalty system: constant, linear and affine; end gap penalties; selection of back-trace priorities, including random one; asymmetric penalty systems for each sequence; possibility of infinite penalty for insertion. The program aligns the sequences in any alphabet what is determined by the scoring matrix. The user interface allows loading the sequence from the FASTA file and presetting the group settings of the program, in particular, copying the default settings of the corresponding Blast or Emboss services. Implementation means that the program does not require installation and runs locally on the client machine parallelizing the specified number of cores using web-worker technologies and using automatic grid step selection to minimize memory. The program was tested to align nucleotide and aminoacid sequences up to the order of 10D. For example, testing was carried out on random sequences that showed a 50 percent similarity regardless of the length at the default settings of algorithm. Parameters of algorithm are presented below in the Table 1.
Table 1 – Required memory, optimal grid step and execution time for different lengths of sequences.

Conflict of Interest
None declared.
Конфликт интересов
Не указан.
References
Needleman S., Wunsch C. A general method applicable to the search for similarities in the amino acid sequence of two proteins. // Journal of Molecular Biology. – 1970. – №3 (48) – P. 443-453.
Pyatkov M.I., Pankratov A.N. SBARS: fast creation of dotplots for DNA sequences on different scales using GA-, GC- content. // Bioinformatics. - 2014. - №12 (30) - P. 1765—1766.
Gotoh O. An improved algorithm for matching biological sequences. // Journal of Molecular Biology. – 1982. - №3 (162) - P. 705–708.
Myers E.W., Miller W. Optimal alignments in linear space. // Computer Applications in the Biosciences. – 1988. - №1 (4) – P. 11–17.
Driga A., Lu P., Schaeffer J., Szafron D., Charter K., Parsons I. FastLSA: A Fast, Linear-Space, Parallel and Sequential Algorithm for Sequence Alignment. // Algorithmica. – 2006. - №3 (45) – P. 337-375.
Galvez S., Diaz D., Hernandez P., Esteban F.J., Caballero J.A., Dorado G. Next-generation bioinformatics: using many-core processor architecture to develop a web service for sequence alignment. // Bioinformatics. – 2010. - №5 (26) – P. 683-686.
Tetuev R.K., Pyatkov M.I., Pankratov A.N. Parallel algorithm for global alignment of long aminoacid and nucleotide sequences. // Mathematical Biology and Bioinformatics. – 2017. - №1 (12) – P. 137-150.
