SS/SW BASE PAIRS ARE THE ONLY BASE PAIRS INVOLVED IN LONG-RANGE RNA TERTIARY MOTIFS
DOI: https://doi.org/10.18454/jbg.2020.1.13.1
Manakov A.K.1, Yakovlev V.V.2, Baulin E.F.*3
1, 2, 3 Moscow Institute of Physics and Technology (National Research University), Dolgoprudny, Russia;
2, 3 Institute of Mathematical Problems of Biology RAS – the Branch of Keldysh Institute of Applied Mathematics of Russian Academy of Sciences, Pushchino, Russia
* Correspodning author (baulin[at]lpm.org.ru)
Received: 16.12.2020; Accepted: 10.01.2020; Published: 20.01.2020
SS/SW BASE PAIRS ARE THE ONLY BASE PAIRS INVOLVED IN LONG- RANGE RNA TERTIARY MOTIFS
Research article
Abstract
The structure of noncoding RNAs largely determines their functions. With the rapid growth of experimental data on the RNA secondary structures, the task of predicting its spatial structure becomes the most urgent task of RNA bioinformatics. The ability to predict tertiary base pairs from data on the secondary structure could significantly reduce the operating time and improve the quality of the RNA spatial structure prediction algorithms. In this work, we applied the machine learning algorithm for the problem of RNA tertiary base pairs prediction from data on the RNA sequence and secondary structure. A group of local base pairs was identified that can be predicted with high quality (80% precision, 80% recall). It was also shown that more than 70% of all long-range noncanonical base pairs in RNA are the base pairs of geometric classes Sugar-Edge/Sugar-Edge and Sugar-Edge/Watson-Crick-Edge that correspond to ribose zipper and A-minor tertiary motifs.
Keywords: RNA structure, secondary structure, base pair, tertiary motif, ribose zipper, A-minor, machine learning.
Манаков А.К.*1, Яковлев В.В.2, Баулин Е.Ф.3
1, 2, 3 Московский физико-технический институт (национальный исследовательский университет), Долгопрудный, Россия
2, 3 Институт математических проблем биологии Российской академии наук - филиал Федерального государственного учреждения «Федеральный исследовательский центр Институт прикладной математики им. М.В. Келдыша Российской академии наук», Пущино, Россия
* Корреспондирующий автора (baulin[at]lpm.org.ru)
Получена: 16.12.2020; Доработана: 10.01.2020; Опубликована: 20.01.2020
ТОЛЬКО SS/SW СПАРИВАНИЯ ОСНОВАНИЙ ВСТРЕЧАЮТСЯ В УДАЛЕННЫХ МОТИВАХ ТРЕТИЧНОЙ СТРУКТУРЫ РНК
Научная статья
Аннотация
Структура некодирующих РНК в значительной степени определяет их функциональность. С ростом экспериментальных данных о вторичных структурах РНК наиболее актуальной задачей биоинформатики РНК становится задача предсказания её пространственной структуры. Возможность предсказывать третичные спаривания оснований по данным о вторичной структуре позволит существенно сократить время работы и повысить качество работы алгоритмов предсказания пространственной структуры РНК. В данной работе алгоритм машинного обучения был использован для решения задачи предсказания третичных спариваний по данным о последовательности и вторичной структуре РНК. Была выявлена группа локальных спариваний, которые могут быть предсказаны с высокой точностью (80% precision, 80% recall). Кроме того, было показано, что среди удалённых неканонических спариваний более 70% составляют спаривания геометрических классов Sugar-Edge/Sugar-Edge и Sugar-Edge/Watson-Crick-Edge, которые соответствуют таким третичным мотивам как рибозные молнии и А-миноры.
Ключевые слова: структура РНК, вторичная структура, спаривание оснований, третичный мотив, рибозная молния, А-минор, машинное обучение.
1. Introduction
Noncoding RNAs comprise one of the most abundant and important classes of biopolymers in living cells. Apart from well- established role of transfer and ribosomal RNAs in protein synthesis [1], various noncoding RNAs take part in numerous biological processes such as gene expression regulation on both transcription [2] and translation levels [3], intron splicing [4], RNA modification [5], transposon control [6] and many others; a number of long noncoding RNAs are linked with several types of cancer [7]. Functions of the RNA molecules are hardly dependent on their spatial structure [8].
Over the past 5 years, experimental methods deriving data on RNA secondary structure have improved dramatically [9]. Coupling with high-throughput sequencing methods made it possible to probe secondary structures of RNA in vivo on a large scale [9]. These data significantly improves the quality of RNA secondary structure prediction tools that allows us to assume that the RNA secondary structure prediction problem will be soon considered sufficiently solved.
At the same time RNA spatial structure prediction algorithms are still far from acceptable quality [10]. Additional constraints can help reduce working time and/or improve the quality of such algorithms [11]. Data on possible noncanonical base pairs derived from experimentally determined RNA spatial structures could be used for this purpose as base pairs are the major type of nucleotide interactions in RNA tertiary structure.
Only two different base pair classifications exist, both being geometric classifications. In [12] authors distinguish 28 possible types of base pairs having at least two hydrogen bonds. All the types are characterized by nucleotide bases, their relative positions and exact pairs of bonded atoms. According to the Leontis-Westhof classification [13], all base pairs are classified into geometric families by interacting edges of nucleotides. Each nucleotide is represented by a triangle with three edges - Sugar edge (S), Hoogsteen edge (H) and Watson-Crick edge (W). A base pair is characterized by two interacting edges of nucleotides and by their relative orientation (cis or trans) making a total of 12 possible families. It should be noted that families do not consider base types.
To the moment there is a lack of classifications of noncanonical base pairs considering their structural context. The only attempt was made in [14] where within the analysis of 16S rRNA authors distinguished local and long-range base pairs and also divided them into three groups considering their role in secondary structure (helix-helix, loop-helix, loop-loop). A base pair was considered long-range if it intersected at least 4 canonical base pairs and considered local otherwise.
In this work, we applied the machine learning algorithm for the problem of de novo predicting tertiary base pairs using the data on RNA sequence and secondary structure. For base pair annotation the original description of RNA secondary structure
[15] was used. To the best of our knowledge, the problem is formulated for the first time. The most similar problem was stated for example in [16] where authors predicted RNA nucleotide-nucleotide contacts using the multiple alignment of RNA sequences.
2. Methods
For the analysis we used experimentally determined RNA spatial structures from the Protein Data Bank (PDB, [17]). We considered two subsets of RNA structures - a representative set ([18], release 3.76 with 3.0Å resolution cutoff) and a non- redundant set. The non-redundant set was selected manually and contained 44 RNA chains (including 23 riboswitches, 7 ribozymes, and 6 ribosomal RNAs, see Additional file 1); the representative set comprised 398 RNA chains containing at least one intramolecular stem (double-helical region).
Base pairs in RNA structures were annotated with the DSSR program from the X3DNA toolkit [19]. The structural context for base pairs was annotated using the generalized description of RNA secondary structure elements from [15]. A base pair was called a tertiary base pair if it was not a part of any stem. A base pair was called noncanonical if it belonged to any type aside from Watson-Crick (GC cWW, AU cWW) and Wobble (GU cWW) types in Leontis-Westhof classification [13].
Two sets of all possible nucleotide pairs were constructed with respect to the two considered sets of RNA structures. For every pair of nucleotides [N1, N2] symmetrical pair [N2, N1] was also in the dataset. A pair [N1, N2] were annotated as positive base pair if a base pair (N1, N2) existed and negative otherwise. To reduce the imbalance of positive and negative classes we removed all pairs where the distance between two nucleotides in RNA sequence was greater than 60 positions, keeping less than 10% of all negative pairs and more than 80% of all positive pairs. The resulted representative set of nucleotide pairs included
~18k positive objects and ~6790k negatives. The non-redundant set included ~4k positives and ~1500k negatives.
Each pair of nucleotides was annotated with the following features:
1. Base type (A/C/G/U/M/N, where M is for modified bases, N is for unknown bases) of interacting nucleotides and their neighbors (20 neighbors in total, 5 neighbors from each side of both nucleotides, applies hereinafter);
2. RNA secondary structure element which interacting nucleotides and their neighbors belong to (stem (S) / hairpin loop (H)
/ Bulge (B) / Internal loop (I) / Multiple junction (J); all loops were also assigned one of three types related to the pseudoknots - Classical (C), Isolated (I), Pseudoknotted (P), such that, for example, nucleotide annotated with HC belongs to a classical hairpin loop);
3. Length of paired/unpaired fragment which a nucleotide belongs to (for interacting nucleotides and their neighbors);
4. Ordinal number of a nucleotide within its paired/unpaired fragment (for interacting nucleotides and their neighbors);
5. The relative position of interacting nucleotides within the secondary structure of RNA (inside one stem or loop (Same, SM) / inside a loop and its adjacent stem (Local, LC), from distant structural elements (Long-range, LR));
6. Whether there is a corresponding base pair (1 or 0, target feature).
To solve the binary classification problem we used the RandomForest algorithm [20] implemented in [21]. All experiments were conducted in the form of GoupKfold cross-validation [21] in order to keep at each step all base pairs belonging to one RNA structure either in the training set or in the test set. For dimension reduction during clusterization of true positives we used the t- SNE technique [22].
3. Results
Cross-validation on the representative dataset showed an acceptable quality of 67%-67% precision-recall metrics (Fig.1a). However, a closer examination of the results identified that RNA molecule types having greater numbers of instances tend to get better results meaning that a great part of success comes from the data redundancy. Due to the observation, only the non- redundant dataset was used for further analysis. Consistently with the observation, the non-redundant dataset demonstrated a significantly lower quality of 35%-35% precision-recall metrics (Fig. 1b).
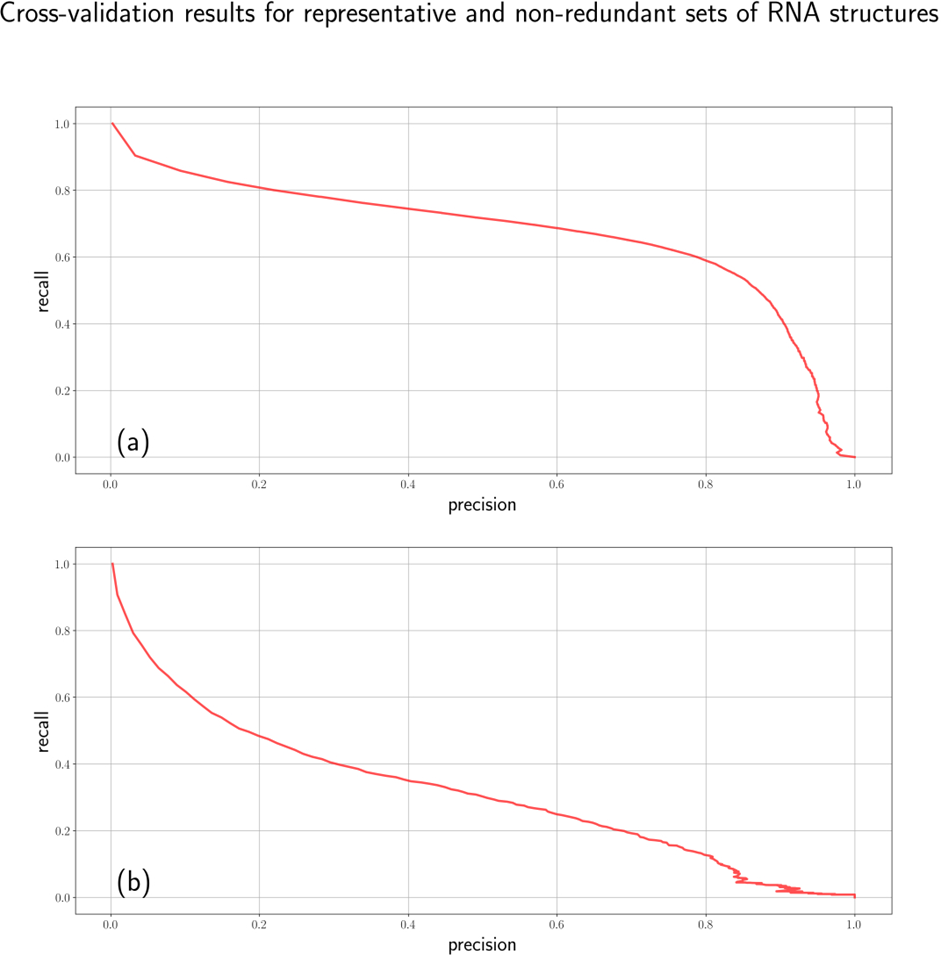
Figure 1 – Precision-recall curves for the representative (a) and non-redundant (b) sets of RNA structures
The obtained results allowed us to speculate that in general tertiary base pairs are poorly predicted based solely on the RNA sequence and secondary structure. An in-depth analysis was performed in order to identify particular classes of base pairs that could be predicted with the described method. The analysis showed that the best results were obtained for tHS (trans H-edge/S- edge) base pairs. Clusterization of the tHS base pairs (Fig. 2, top) emphasized two ellipses with the only base pair predicted wrong. The ellipses correspond to the AG tHS base pairs from the same classical hairpin loop being a GNRA-like motif [23]. Cross-validation on the dataset of AG SM-HC pairs resulted in 80%-80% precision-recall metrics (Fig. 2, bottom).
In total, we were able to identify few classes that could be predicted with acceptable quality (better than 50%-50% precision- recall metrics), namely AG and AU pairs from the same classical hairpin (AG SM-HC, AU SM-HC) and arbitrary pairs of bases within a classical internal loop (SM-IC).
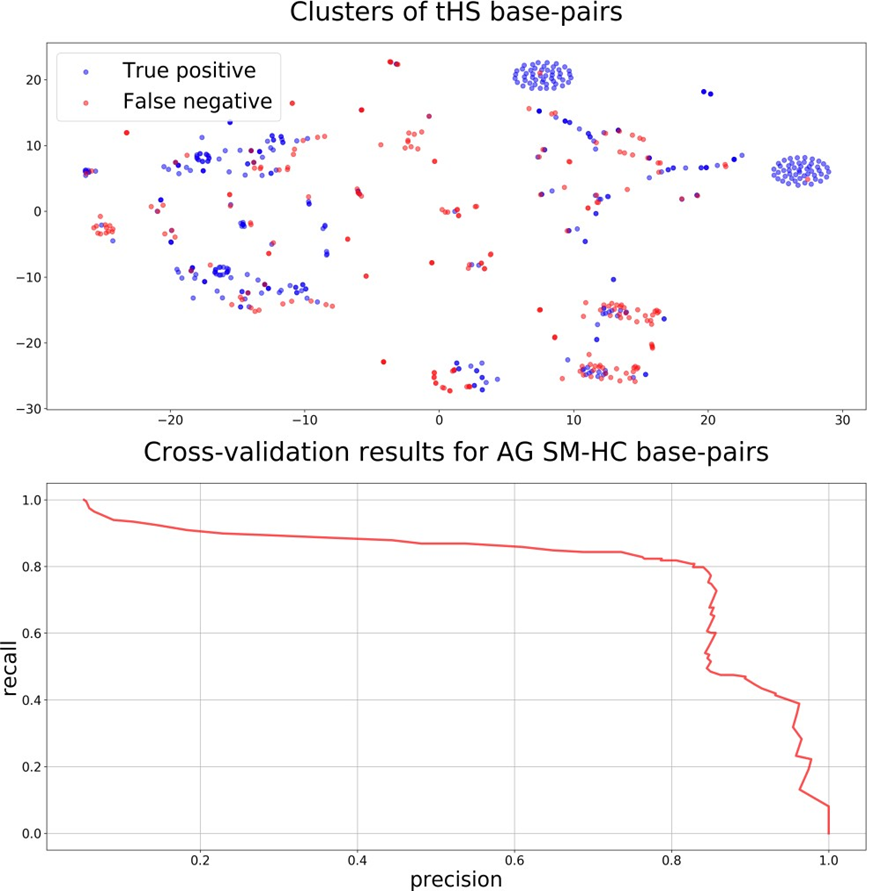
Figure 2 – Identification and prediction of tHS AG base pairs from GNRA-like motifs:
top: clusters of all positive tHS base pairs colored by their predicted classes. Two symmetrical ellipses correspond to AG tHS base pairs from GNRA-like hairpin loops. bottom: cross-validation results on the dataset containing only AG pairs from the same hairpin
To explain tHS base pairs being the best-predicted type we calculated the distribution of structural classes within each possible geometrical class coupled with a pair of bases (Fig. 3). Sequence distance cutoff was not applied allowing all base pairs present in the RNA structures for calculations. The results showed that 95% of tHS base pairs being of SM class is the reason the tHS base pairs are best predicted. In general, only 80% of tertiary base pairs belong to the SM class. Another important feature is that AG/GA comprise almost 80% of all tHS base pairs. From that, we can conclude that tHS base pairs are highly specific for GNRA-like motifs and are hardly rare among long-range base pairs.
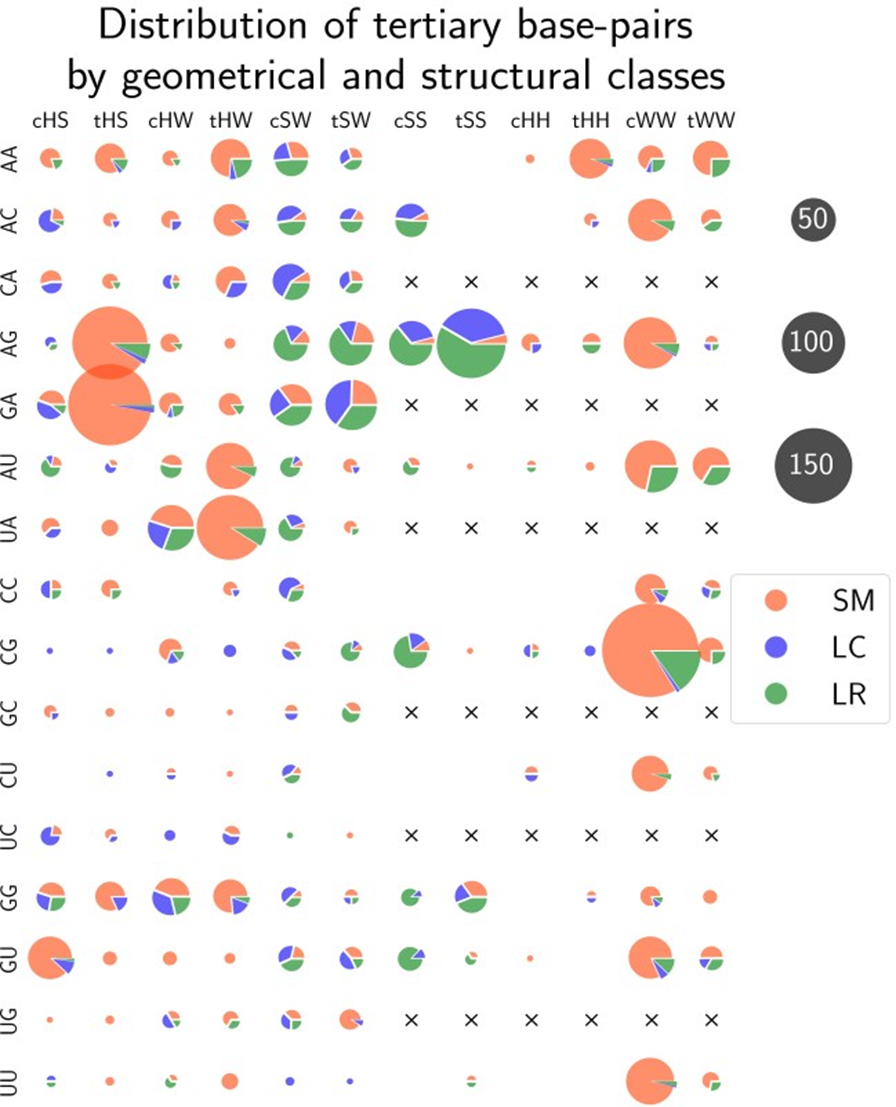
Figure 3 – Distribution of all tertiary base pairs from the non-redundant dataset by geometrical and structural classes: The total number of base pairs is 2591. Black crosses represent redundant pairs of bases in case of symmetrical types (SS, HH, WW). Numbers of base pairs are proportional to the circle areas
Interestingly, more than 70% of all long-range noncanonical base pairs belong to 4 geometrical families - cSS, tSS, cSW, tSW (see Fig. 3, green segments). These families correspond to the only two types of long-range RNA tertiary motifs - ribose zippers [24] and A-minors [25]. We also noted that 65% of all tertiary base pairs contain adenine as one of their interacting bases. It is in agreement with the fact that adenine is overrepresented in unpaired regions of noncoding RNAs [25].
Supplementary materials
Additional file 1 (xlsx): Table S1. Non-redundant set of RNA structures.
Acknowledgments
Authors thank Ivan Kulakovskiy for valuable comments.
Conflict of Interest Конфликт интересов
None declared. Не указан.
References
Watson J. D. Involvement of RNA in the Synthesis of Proteins: The ordered interaction of three classes of RNA controls the assembly of amino acids into proteins //Science. – 1963. – Т. 140. – №. 3562. – С. 17-26. https://doi.org/10.1126/science.140.3562.17
Hollands K. et al. Riboswitch control of Rho-dependent transcription termination //Proceedings of the National Academy of Sciences. – 2012. – Т. 109. – №. 14. – С. 5376-5381. https://doi.org/10.1073/pnas.1112211109
Breaker R. R. Riboswitches and translation control //Cold Spring Harbor perspectives in biology. – 2018. – Т. 10. – №. 11. – С. a032797. https://doi.org/10.1101/cshperspect.a032797
Dvinge H. et al. RNA components of the spliceosome regulate tissue-and cancer-specific alternative splicing //Genome research. – 2019. – Т. 29. – №. 10. – С. 1591-1604. https://doi.org/10.1101/gr.246678.118
Kiss T. Small nucleolar RNA‐guided post‐transcriptional modification of cellular RNAs //The EMBO journal. – 2001. – Т. 20. – №. 14. – С. 3617-3622. https://doi.org/10.1093/emboj/20.14.3617
Aravin A. A. et al. Developmentally regulated piRNA clusters implicate MILI in transposon control //Science. – 2007. – Т. 316. – №. 5825. – С. 744-747. http://doi.org/10.1126/science.1142612
Yang G., Lu X., Yuan L. LncRNA: a link between RNA and cancer //Biochimica et Biophysica Acta (BBA)-Gene Regulatory Mechanisms. – 2014. – Т. 1839. – №. 11. – С. 1097-1109. https://doi.org/10.1016/j.bbagrm.2014.08.012
Montange R. K., Batey R. T. Riboswitches: emerging themes in RNA structure and function //Annu. Rev. Biophys. – 2008. – Т. 37. – С. 117-133. https://doi.org/10.1146/annurev.biophys.37.032807.130000
Strobel E. J., Angela M. Y., Lucks J. B. High-throughput determination of RNA structures //Nature Reviews Genetics. – 2018. – Т. 19. – №. 10. – С. 615-634. https://doi.org/10.1038/s41576-018-0034-x
Miao Z. et al. RNA-Puzzles Round III: 3D RNA structure prediction of five riboswitches and one ribozyme //Rna. – 2017. – Т. 23. – №. 5. – С. 655-672. https://doi.org/10.1261/rna.060368.116
Wang J. et al. Limits in accuracy and a strategy of RNA structure prediction using experimental information //Nucleic acids research. – 2019. – Т. 47. – №. 11. – С. 5563-5572. https://doi.org/10.1093/nar/gkz427
Saenger W. Principles of nucleic acid structure. – Springer Science & Business Media, 2013. https://doi.org/10.1007/978-1-4612-5190-3
Leontis N. B., Westhof E. Geometric nomenclature and classification of RNA base pairs //Rna. – 2001. – Т. 7. – №. 4. – С. 499-512. https://doi.org/10.1017/S1355838201002515
Sweeney B. A., Roy P., Leontis N. B. An introduction to recurrent nucleotide interactions in RNA //Wiley Interdisciplinary Reviews: RNA. – 2015. – Т. 6. – №. 1. – С. 17-45. https://doi.org/10.1002/wrna.1258
Baulin E. et al. URS DataBase: universe of RNA structures and their motifs //Database. – 2016. – Т. 2016. https://doi.org/10.1093/database/baw085
Jian Y. et al. DIRECT: RNA contact predictions by integrating structural patterns //BMC bioinformatics. – 2019. – Т. 20. – №. 1. – С. 1-12. https://doi.org/10.1186/s12859-019-3099-4
Rose P. W. et al. The RCSB Protein Data Bank: redesigned web site and web services //Nucleic acids research. – 2010. – Т. 39. – №. suppl_1. – С. D392-D401. https://doi.org/10.1093/nar/gkq1021
Leontis N. B., Zirbel C. L. Nonredundant 3D structure datasets for RNA knowledge extraction and benchmarking //RNA 3D structure analysis and prediction. – Springer, Berlin, Heidelberg, 2012. – С. 281-298. https://doi.org/10.1007/978-3-642-25740-7_13
Lu X. J., Bussemaker H. J., Olson W. K. DSSR: an integrated software tool for dissecting the spatial structure of RNA //Nucleic acids research. – 2015. – Т. 43. – №. 21. – С. e142-e142. https://doi.org/10.1093/nar/gkv716
Liaw A. et al. Classification and regression by randomForest //R news. – 2002. – Т. 2. – №. 3. – С. 18-22. https://www.bibsonomy.org/bibtex/2ba2e49a65786a6ff232994289edb42f3/lukasbeckmann
Pedregosa F. et al. Scikit-learn: Machine learning in Python //Journal of machine learning research. – 2011. – Т. 12. – №. Oct. – С. 2825-2830. http://www.jmlr.org/papers/v12/pedregosa11a
Maaten L., Hinton G. Visualizing data using t-SNE //Journal of machine learning research. – 2008. – Т. 9. – №. Nov. – С. 2579-2605. http://www.jmlr.org/papers/v9/vandermaaten08a.html
Heus H. A., Pardi A. Structural features that give rise to the unusual stability of RNA hairpins containing GNRA loops //Science. – 1991. – Т. 253. – №. 5016. – С. 191-194. https://doi.org/10.1126/science.1712983
Tamura M., Holbrook S. R. Sequence and structural conservation in RNA ribose zippers //Journal of molecular biology. – 2002. – Т. 320. – №. 3. – С. 455-474. https://doi.org/10.1016/S0022-2836(02)00515-6
Nissen P. et al. RNA tertiary interactions in the large ribosomal subunit: the A-minor motif //Proceedings of the National Academy of Sciences. – 2001. – Т. 98. – №. 9. – С. 4899-4903. https://doi.org/10.1073/pnas.081082398
