THE GENOTYPE-PHENOTYPE RATIO DETERMINED BY GEOMETRIC MORPHOMETRY

DOI: https://www.doi.org/10.18454/jbg.2023.20.2.003

Baranov S.G. *

Vladimir State University, Vladimir, Russia

* Corresponding author (bar.serg58@gmail.com)

Received: 04.04.2023; Accepted: 19.05.2023; Published: 26.05.2023

THE GENOTYPE-PHENOTYPE RATIO DETERMINED BY GEOMETRIC MORPHOMETRY

Research article

Abstract

Phenotypic and genotypic variability are manifested in the shape, size and asymmetry of laminas. To describe the reaction of plants to geographical location, a linear modelling of the shape and asymmetry of laminas of two types of trees was carried out: light-demanding (Bird cherry, Prunus padus) and shade-resistant (small-leaved linden, Tilia cordata Mull). 8 cenopopulations were selected, located from north to south (from Murmansk to Moscow Oblast). In the linden tree, the distance between the bases of the veins were measured, and the bird cherry – the leaf width. Linear signs R (right) L (left) showed no correlation (Spearman's r >0.05) with the index of fluctuating asymmetry |R – L|/(R + L). 100 labels were placed along the sheet contour, and a morphogeometric 2-factor analysis of variance (MorphoJ) was performed. The index of fluctuating asymmetry of FA18 was calculated taking into account the error of threefold labelling, and the p-level taking into account the correction α = 0.05 for the entire range of FA values for seven populations. Directional asymmetry was determined by the criterion F of the "side" factor. The correlation coefficient r was found between the diagonal values of the phenotype and genotype matrices. The obtained values of fluctuating asymmetry, directional asymmetry and phenotype/genotype correlation were multiplied to n =50 taking into account the normal distribution, and linear approximation was performed (R ² = 0.97-0.99). The trend lines were arranged in descending order. The regression coefficients were evaluated according to the F-criterion for the difference in the residuals' variance. The laminas of the small–leaved linden showed a higher fluctuation asymmetry, the leaves of the bird cherry showed a greater directional asymmetry. The phenotype/genotype ratio also was different in the two species (p <0.05). Northern linden populations ( Petrozavodsk and Apatity) showed a higher index compared to the southern populations from Moscow Oblast (Mozhaysk), respectively, FA18 = 0.0002; p = 0.01 and FA18 = 0.0001; p = 0.02. A high proportion of the variability of directional asymmetry as a genotypic manifestation was manifested in bird cherry as a local species. Small-leaved linden as an introduced species showed phenotypic variability, with a high proportion of fluctuating asymmetry. The data obtained indicated a different reaction of the genotype and phenotype of the two species, depending on the geographical location of the cenopopulations.

Keywords: asymmetry, matrix, phenotype-genotype model.

Баранов С.Г. *

Владимирский государственный университет, Владимир, Россия

* Корреспондирующий автор (bar.serg58@gmail.com)

Получена: 04.04.2023; Доработана: 19.05.2023; Опубликована: 26.05.2023

СООТНОШЕНИЕ ГЕНОТИП-ФЕНОТИП, ОПРЕДЕЛЯЕМОЕ ГЕОМЕТРИЧЕСКОЙ МОРФОМЕТРИЕЙ

Научная статья

Аннотация

Фенотипическая изменчивость и генотипическая изменчивость проявляются в форме, величине и асимметричности листовых пластин. Для описания реакции растений на географическое местоположение было проведено линейное моделирование формы и асимметрии листовых пластин двух видов деревьев: светолюбивого (Черемуха обыкновенная, Prunus padus) и теневыносливого (Липа мелколистная, Tilia cordata Mull). Были выбраны 8 ценопопуляций, располагавшихся с севера на юг (от г. Мурманск до Московской области). У липы измерялось расстояние между основаниями жилок, а у черемухи – ширина листа. Линейные признаки R (правый) L (левый) не показали корреляционной связи (Spearman’s r >0.05) с индексом флуктуирующей асимметрии |R – L|/(R + L). По контуру листа выставлялось 100 меток и проводился морфогеометрический 2-х факторный дисперсионный анализ (MorphoJ). Индекс флуктуирующей асимметрии ФА18 рассчитывался с учетом ошибки троекратного нанесения меток, а р-уровень с учетом поправки α = 0.05 на весь ряд значений ФА для семи популяций. Направленная асимметрия определялась по критерию F фактора «сторона». Находился коэффициент корреляции r между диагональными значениями матриц фенотипа и генотипа. Полученные значения флуктуирующей асимметрии, направленной асимметрии и корреляции фенотип/генотип размножались до n =50 с учётом нормального распределения, и выполнялась линейная аппроксимация (R² = 0.97-0.99). Линии трендов располагались по нисходящему значению. Оценка регрессионных коэффициентов проводилась по F-критерию различия дисперсии остатков. Листовые пластины липы мелколистной показали более высокую флуктуационную асимметричность, листья черемухи – большую направленную асимметрию. Коэффициент фенотип/генотип также различался у двух видов (p <0.05). Северные популяции липы (гг. Петрозаводск и Апатиты) показали больший индекс по сравнению с южными популяциями из Московской области (Можайск), соответственно, FA18 = 0.0002; p = 0.01 и FA18 = 0.0001; p = 0.02. Высокая доля изменчивости направленной асимметрии как генотипического проявления проявился у черемухи, как местного вида. Липа мелколистная как вид-интродуцент проявлял фенотипическую изменчивость с высокой долей флуктуирующей асимметрии. Полученные данные свидетельствовали о различной реакции генотипа и фенотипа двух видов в зависимости от географического расположения ценопопуляций.

Ключевые слова: асимметрия, матрица, модель фенотип-генотип.

1. Введение

Стабильность развития популяций определяется по величине флуктуирующей асимметрии (ФА) как различия в правых и левых билатерально симметричных структурах. Изучение ФА проводится не менее 30 лет с использованием как счетных, так и мерных признаков. Распространенной практикой является сравнение стабильности развития контрольных и экспериментальных территорий, когда отбираются листовые пластины с древесных ценопопуляций вдоль градиента техногенного стресса. Другие работы включают тестирование ФА в природных популяциях с разными условиями среды (широтная и высотная поясность, географически разобщенность и световой режим) [1].

Исследователи не пришли к однозначному мнению о генетической природе ФА. Устоявшимся положением считается возможный эпистатический ответ генов на влияние среды, в отличие от других видов асимметрии – направленной и антисимметрии, связанных с генетической предрасположенностью, а также дискутируется эпигенетическое влияние на ранних стадиях развития мерономных структур растений [2]. Одновременно обсуждается роль пластической изменчивости и сопряженность ее по отношению к билатеральной флуктуации гомологичных признаков [3].

Методы моделирования широко используются для прогнозирования реакции организма на внешние и эндогенные факторы, в том числе при выборе методов эффективного тестирования ФА при различных выборочных свойствах полевых данных [4], [5].

Изучение стабильности развития растений сталкивается с проблемой морфологического разнообразия, например, листовых пластин, а также разнообразия их размеров и билатеральных гомологичных признаков. Обычно тестирование ФА включает обязательный элемент поиска связи размер признака – ФА. Этот прием помогает исключить связь между величиной признака и уменьшением/увеличением асимметричности.

Неоднозначность результатов может обескураживать: в сильнозагрязненных районах ФА может быть значительно ниже, чем в импактных зонах, даже при работе с такими признанными индикаторами стабильности развития как береза повислая [2].

Понятие «траектория развития» популяции обозначает как филогенетический путь развития, так и от онтогенетических свойств (в большей степени), таких, как свойства семян растения, первоначальные условия развития семени, закладки листа и развития проростка. Синергетические условия, связанные с климатом, особенно в стадии весенней вегетации в совокупности с факторами техногенной нагрузки и рельефа оказывают воздействие на морфологические, размерные и структурные особенности листовой пластины.

Среди разнообразных факторов, влияющих на пролиферацию листовой пластины, важным представляется способность к фотосинтезу в различных экологических группах. Высоко светолюбивые гелиофиты, включая черемуху обыкновенную, (Prunus padus L., 1753, f. Rosaceae) обладают более мелкими и жесткими листьями. Теневыносливые древесные виды, липа мелколистная в том числе, могут фотосинтезировать даже при 1-5 % от внешнего освещения, отсюда высокое проявление направленной асимметрии (НА), т.е. сдвига разности величин правого и левого признака в одну из сторон. Чаще доминирует левая половина, т.к. как происходит спиральная закладка побегов снизу – верх и слева – направо. Нижняя сторона /левая половина стремится к солнцу по восходящей спирали. Описанная система организации побегов характерна для липы мелколистной (Tilia cordata Mill., f. Malvaceae), обладающей широкой адаптационной реакцией в ответ на освещенность. С другой стороны, широкий диапазон реакции удобен для тестирования ФА, а точнее соотношения НА/ФА, составляющих общую асимметрию. Известно, что антисимметрия как статистически значимое явление встречается крайне редко.

Черемуха обыкновенная, в отличие от липы мелколистной, обладает более широким ареалом, включающим Кольский полуостров. г. Мурманск – самая северная заполярная точка распространения этого вида. Липу мелколистную следует считать интродуцентом. Известно, что для форпостных популяций, в данном случае – черемухи, листовые пластины в силу адаптации обладают повышенной морфологической изменчивостью и высоким морфоразнообразием [6], [7].

Предыдущие работы показали, что в северных популяциях форма пластин отличалась повышенной пластической изменчивостью у обоих видов, как у локального, так и у интродуцированного вида. В отношении величины ФА результаты показали различный уровень асимметрии в зависимости от года сбора листовых пластин [8]. Целью этой работы было сравнение координат векторов меток, показывающих общую изменчивость формы и асимметрическую изменчивость. В задачу входило сравнение корреляционной матрицы фенотип/генотип значениями индексов ФА и индексов направленной асимметрии. Таким образом, предполагалось нахождение связи между фенотипической и генотипической изменчивостью в листовых пластинах двух видов растений, различных по реакции на внешние условия среды.

2. Методы исследования

2.1. Места сбора

Листовые пластины собирались в августе-сентябре в 2021-2022 гг. с нижней кроны дерева генеративной стадии роста с размерами, характерными для изучаемых популяций. Сбор проводился 2 раза с перерывом 1-2 недели по 5 пластин с каждого из десяти деревьев со всех сторон кроны. Были выбраны города в различной географической поясности, с различными физико-географическим рельефом и условиями среды в направлении с севера на юг: Мурманск-Апатиты-Петрозаводск-Санкт-Петербург. Мурманск (68°58′00′′ с.ш.) имел комплексный индекс загрязнения атмосферы 2,99). г. Апатиты (67°34′03″ с. ш.) был более благополучен по состоянию воздуха (комплексный индекс загрязнения атмосферы города – 1,25, что ниже среднего по стране). г. Петрозаводск (61°47′46′′ с. ш.) считается неблагополучным из-за загрязнения почвы свинцом и цинком сверх предельно допустимой концентрации, особенно в верхних слоях почвы, вдоль автомобильных и железнодорожных магистралей. Санкт-Петербург (59°57′с.ш.) – наиболее густонаселенный мегаполис с влажным климатом обладал специфической урбосредой с неравномерным распределением поллютантов и источников техногенного стресса. В качестве контрольных использовались популяций растений средней полосы России из гг. Можайск 55°30′ с.ш., Электросталь (55°48′ с. ш.), (Московская обл.) и гг. Муром (55°34′ с. ш.), и Владимир (Владимирская обл.; 56°08′ с. ш.).

2.2. Статистическая обработка и моделирование

Листья сканировались с разрешающей способностью 300 dpi. У листьев липы измерялся 4-й признак (основание 1-й 2-й жилок), у листьев черемухи измерялась половина листа, как наиболее доступный линейный признак.

 Измерения проводились троекратно дигитайзером TPSdig2 (Rholf,2017) и результаты измерений (в см) сначала заносились в таблицы Excel, затем – в таблицы STATISTICA 10 (Statsoft Ink.), где выполнялись анализы описательной статистики (discriptive statistics) и основные тесты (basic statistics).

Для определения ФА методом геометрической морфометрии использовалась программа MorphoJ (Klingenberg, 2019). Оценка асимметрии по форме листовых пластин проведена с помощью эталона, усредненного консенсуса, т.е. формы, полученной после усреднения форм всех образцов листьев. Наносились по 50 меток на каждой половине листа, две метки в основании и в верхушке служили для создания оси симметрии. Конфигурация выравнивалась и служила для регистрации векторов с координатами ХУ.

Для проверки на выбросы квадратичные прокрустовы дистанции откладывались по оси ОХ, а по оси ОУ – кумулятивные частоты. Накопительные частоты визуально соответствовали модельному интегративному графику, и выбросов обнаружено не было.

Проводился дисперсионный анализ с учетом дисперсии координат меток и определялись морфогеометрические индексы НА и ФА (ФА18). Как и в тривиальном 2-х факторном анализе, для тестирования ФА показатель F_I×S Goodall’s, находился отношением средних квадратов (MS) взаимодействия лист и сторона (I×S) к MS ошибки измерения, а для определения направленной асимметрии (Fs) средний квадрат MS фактора «сторона» относился к MS ошибки измерения MS_error. Уровень р для ФА18 находился исходя из F- распределения значений F_I×S и степеней свободы df взаимодействия I×S и df ошибки [10], [11].

Проводилась корректировка Бонферрони с учетом наибольшего уровня р, который принимался за 0.05. Окончательным индексом ФА18 служила разность MS_I×S минус MS_error отнесенная к числу измерений, т.е. к трем. Экспериментальной единицей служила листовая пластина, а статистическая значимость оценивалась на уровне 95%.

Для соотношения фенотип/генотип использовались корреляционные матрицы координат векторов. Матрица формы относилась к матрице асимметрии, и находился коэффициент корреляции r как среднее диагональных коэффициентов [9]. Полученный коэффициент сравнивался с коэффициентом F для обоих видов асимметрии из Прокрустового дисперсионного анализа. Для этого величины ФА и НА генерировались в виде нормально распределенных выборок с учетом среднего и стандартного отклонения с n = 50. Выборки располагались в порядке убывания значений и строились линии тренда с линейной аппроксимацией. Находились степень аппроксимации и коэффициент угла наклона k из уравнения регрессии.

3. Результаты

Линейные признаки листовых пластин различались по величине среди популяций. Индекс ФА2 = |R– L|/(R + L) не показал значимой корреляции с размером признака (R + L) /2 (Spearman’s r >0.05). Тест Колмогорова-Смирнова выявил отклонение от нормального распределения индекса ФА2 (p <0.05). По результатам морфогеометрического 2-х факторного анализа были получены значения F и матричный корреляционный коэффициент, r и сгенерированы выборки с нормальным распределением для оценки регрессионных моделей.

Результаты моделирования значений, полученных в АНОВА представлены на графике (Рисунки 1, 2).

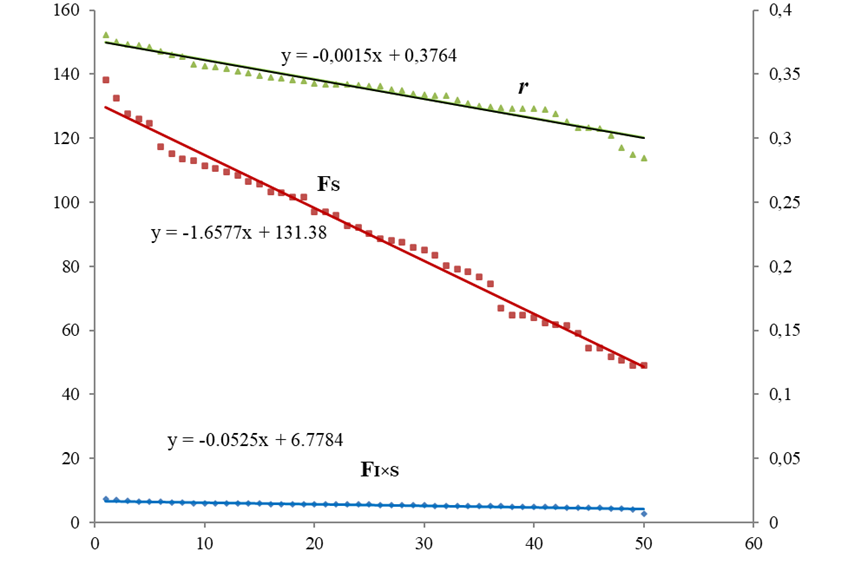
Рис. 1 – Регрессионные зависимости между формой/асимметрией (r) и ФА (F_I×S) и НА (F_S) для Prunus padus:

по оси ОУ слева – НА и ФА, справа – r

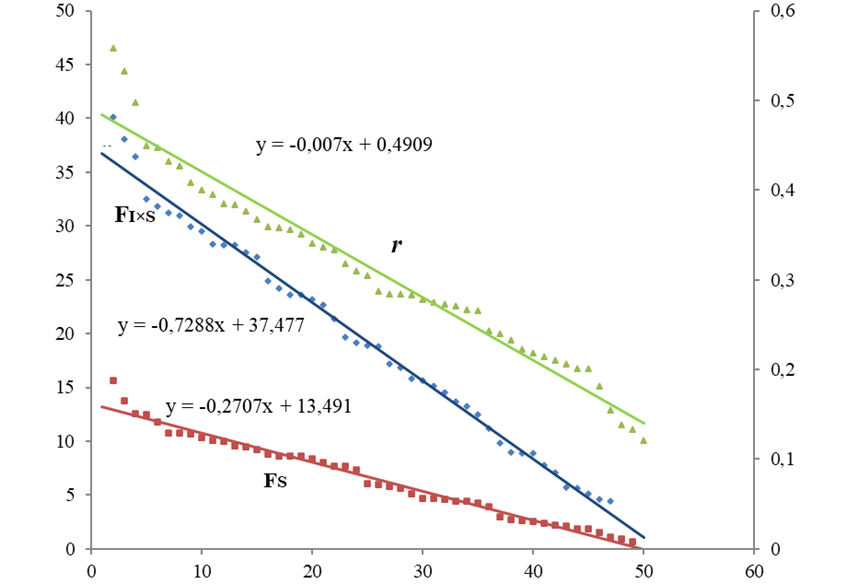
Рис. 2 – Регрессионные зависимости между формой/асимметрией (r) и ФА (F_I×S) и НА (F_S) для Tilia cotdata:
по оси ОУ слева – НА и ФА, справа – r

Все линии линейного тренда показали высокую аппроксимацию (R² = 0.97-0.99), а оба графика показывают высокую корреляцию между тремя трендами (Пирсона r = 0.95-0.98; p <<0.05). Рисунок 1 (черемуха) показывает высокую корреляцию между соотношением матриц и направленной асимметрией и слабую изменчивость флуктуирующей асимметрии: прямая F_I×S меньше по значениям и по вариации по сравнению с листьями липы

У черемухи наибольший наклон прямой Fs, (k = -1.76), что говорит о сильном проявлении направленной асимметрии. У липы мелколистной были характерны высокая ФА и низкое проявление направленной асимметрии.

В обобщенной линейной модели на ФА листьев черемухи большое влияние оказывало величина r корреляционной матрицы форма/асимметрия (F =877; p <<0.05), чем направленная асимметрия (F =471.3; p <<0.05). На ФА листьев липы большее влияние оказывала направленная асимметрия (F =3904; p <<0.05), чем величина r корреляционной матрицы (F =1815; p <<0.05). Статистика Дарбина-Уотсона остатков показала существенную автокорреляцию между ФА и НА (индекс DW был существенно меньше табличного).

Различие в угле наклона регрессии проверялось критерием Фишера сравнением остаточных дисперсий. Сумма квадратов остатков регрессии ФА для липы превышала таковое у черемухи. В отношении регрессии НА – наоборот, доминировала липа мелколистная. По матричному коэффициенту корреляции SS был выше у липы, чем у черемухи (везде p <0.05). Таким образом, соотношение форма/асимметрия у видов были различны. У липы – большая изменчивость ФА. В листьях черемухи – большая изменчивость направленной асимметрии.             

4. Заключение

Учитывая высокую степень свободы и ошибку измерения в северных районах (Апатиты, Петрозаводск) индекс флуктуирующей асимметрии липы мелколистной был равен ФА18 = 0.0002 –0.0003. В районах средней полосы этот индекс был меньше (ФА18 = 0.0001). Не всегда высокое значение FI×S сопровождалось высоким индексом ФА18. Самому высокому значению ФА18 соответствовала ошибка измерения 2.7% от дисперсии разности левых и правых координат. Максимальная ошибка 20,2% соответствовала ФА18 = 0.0001 (везде с высоким уровнем статистической значимости р < 0.000). Высокое значение степени свободы (более 4000) свидетельствовало о высокой точности индекса. Листовые пластины черемухи, как гелиофита, обладали низким индексом ФА18 = 0.0002, равномерно во всех территориях, что свидетельствовало об отсутствии серьезных отклонений в стабильности развития, в отличие от липы мелколистной.

Построенные линейные тренды свидетельствовали о различии двух древесных видов в форме и асимметричности листовых пластин и их адаптивных таксономических особенностях. В проведенном исследовании было использовано морфологические характеристики листовых пластин. Как показали работы с листьями березы повислой, существует существенное расхождение результатов тестирования ФА в зависимости от признаков [2]. Счетные признаки (число зубчиков или число жилок) отражают структурные особенности развития, поэтому в последующих исследованиях буде иметь значение тестирование асимметрии и с учетом меристематических признаков.

Conflict of Interest	Конфликт интересов
None declared.	Не указан.