FALSE TREND AND FREQUENCY REGRESSION APPROACH. EXAMPLE OF AN OCCUPATIONAL RISK STUDY

Частотным (frequency) подходом называют набор статистических приёмов обработки больших массивов эмпирических данных, которые разработаны в значительной мере под влиянием широко известных статистиков К. Пирсона и Р. Фишера. Возможно, Рональду Фишеру наука обязана в большей степени, чем кому-либо еще, за то, какими статистическими методами исследователи пользуются в настоящее время. К современной статистике часто применяется даже термин «фишеровская» в противовес термину «байесовская», введенному самим Р. Фишером, использовавшим последний термин (Bayesian) исключительно в уничижительном смысле как противопоставление своему единственно верному объективному подходу, свободному от субъективных домыслов.

Нисколько не отрицая мотивов названых учёных, следует отметить, что фишеровские методы хорошо работают при наличии действительно большого количества наблюдений, которые не всегда доступны в достаточном объеме. Характерной отраслью медицинской и биологической науки, для которой такая ситуация типична, являются исследования профессионального риска врачами-гигиенистами, токсикологами или эпидемиологами, предпринимаемыми для оценки специфического вредного действия производственных ядов на организм. Изучаются: возникновение сенсибилизирующих, канцерогенных, гонадотропных, эмбриотропных, тератогенных, мутагенных, кардиоваскулярных, склеротических и других отдаленные эффекты, которые в нормальных когортах могли бы возникать также и спонтанно, по мере увеличения возраста. Заметим, что пристальный анализ такого рода производственного вреда характерен для условий, когда и спонтанные, и индуцированные события являются редкими, то есть когда прямая связь между воздействием токсиканта и отдаленным эффектом может быть не очевидна. В противном случае соответствующая производственная технология была бы запрещена без каких-либо статистических исследований. Наблюдение малого количества специфических случаев затрудняет применение фишеровского подхода.

Другим фактором, снижающим мощность статистического исследования профессиональных рисков, является зависимость интенсивности возникновения вредных эффектов от дозы токсиканта. По технологическим причинам полученная или накопленная доза будет различна у разных членов когорты на разных производственных участках. Разным будет и достигнутый вред. Следовательно, возникает задача выявления тренда «доза — эффект», без идентификации которого невозможна эффективная организация управления рисками на основе нормирования предельных доз или экспозиций. Чтобы выявить тренд, исследователю необходимо стратифицировать изучаемый контингент производственной когорты по уровням воздействия, что является серьёзной причиной сокращения статистики «случаев» в каждой страте — на порядок величины, по меньшей мере.

В предлагаемой работе на примере поперечного когортного эпидемиологического исследования будет показано, что в таких ситуациях применение традиционного частотного подхода способно приводить к порождению ложных трендов «доза — эффект». Такая тенденция характерна даже при применении весьма продвинутых методов максимального правдоподобия, предназначенных для многофакторной регрессии. Искажения тренда вызываются появлением систематического смещения точечных оценок из-за малой статистики «случаев» в стратах. Цель статьи заключается в демонстрации этого утверждения. Также будет показано, что применение байесовского подхода к оценке первичных стратифицированных данных в некоторой мере способно устранить систематические искажения на основе иного принципа исследования, сочетающего измерение со статистическим (вероятностным) моделированием в условиях недостатка информации.

В узком смысле изучение зависимости «доза — эффект» необходимо для определения интервала безопасных доз токсикантов. Для этой цели наиболее известно применение методов Беренса, Кербера, Першина, Беренса и Шлоссера, пробит-анализа Миллера и Тейтнера, Лигчфилда и Уилкоксона, метод Штабского

Чтобы получить представление об имеющемся статистическом материале и типовом способе извлечения из него нужной информации, сначала применим методологию AMFIT/Epicureк оценке данных, собранных в результате поперечного исследования интенсивности изучаемой и впервые регистрируемой хронической заболеваемости в однородной возрастной группе работников некоторого предприятия с возрастом от 50 до 55 неполных лет. Выделение этой группы подразумевает, что стаж работников достаточен как для накопления некоторой (неодинаковой) дозы токсиканта, так и для проявления вредного эффекта. Априорно предполагается, что доза не имеет случайной погрешности измерений, а иных факторов риска, кроме дозы и возраста не имеется. Первичные данные представлены в Таблице 1.

Их особенностью является отсутствие статистически значимого отличия данных из страт с номерами 1–10 от данных из нулевой страты. Это — следствие недостаточного числа «случаев» для попарного сравнения, то есть следствие редкости наблюдений. Для оценки тренда больше подошёл бы агрегированный анализ всей таблицы одновременно. При этом можно рассчитывать на уменьшение интервалов неопределенности отношения интенсивностей приблизительно в √10 раз. В этом можно убедиться, формально используя известные частотные тесты Cochran−Armitage

2.1. Оценка тренда «доза — эффект» методом максимального правдоподобия

Центральной идеей алгоритма AMFIT является опора на известную

(1)

Согласно Р. Фишеру, с учетом (1) исследователем формируется функция правдоподобия, в которой все данные таблицы первичных наблюдений фиксируются, а фактически неизвестные значения hk заменяются объединённой моделью тренда h(β | Dk), где Dk — доза в произвольной k-й страте; β-вектор подгоночных параметров. Параметры следует выбрать так, чтобы максимизировать функцию правдоподобия, составленную из произведений (1) по всей эмпирической таблице:

(2)

Максимизация правдоподобия L эквивалентна минимизации функционала оценки качества аппроксимации Ω(β | Data)=-2 ln⁡(L(β | Data)). В силу характера группировки наблюдений, Ω(β | Data) обладает минимальным значением для очень широкого класса моделей, то есть — некоторой точкой насыщения. В ней достигается интерполяция hk=nk/Ak по каждой страте — в соответствии с эвристическим частотным (фишеровским) подходом к оценкам страт по отдельности и в соответствии с известным традиционным эпидемиологическим «определением» интенсивности событий в качестве отношения числа случаев к числу человеко-лет наблюдения

Например, не останавливаясь на подробностях математических выкладок, для простейшей (нулевой, H0) модели тренда h=β0, т.е. для гипотезы о независимости заболеваемости от дозы, минимальная девиация, отсчитанная от точки насыщения, составит , что меньше числа степеней свободы df=10. Это – хороший результат, свидетельствующий о том, что вся совокупность наблюдений в стратах не имеет грубого противоречия гипотезе о постоянстве интенсивности заболеваемости h≈34,4 (на 10 000 человеко-лет наблюдения), если не найдется статистически значимо отличающейся гладкой модельной аппроксимации (H1) с заметно лучшим качеством. Оказывается, такая модель есть: h(β | D)=β0⋅(1+β1⋅D). Для неё  с выигрышем в 7,63 единиц. То есть, достигнуто значение p = 0,0058, указывающее на значимость линейной поправки к дозовому тренду. Это близко к оценкам по тестам Mantel и Cochran-Armitage, отличающимся только выбором функционала оценки качества. Множитель (1+β1⋅D) удобно характеризовать как относительный риск (RR) или отношение интенсивностей (HR, hazard ratio), а β1=ERR/D=0,638 — дозовый коэффициент тренда или избыточный относительный риск, приходящийся на единицу дозы. Параметр β0≈26,8 (на 10 000 человеко-лет) — оценка фоновой интенсивности заболеваемости для рассматриваемого возрастного диапазона.

Полученные результаты понадобятся нам как эталон для сравнения с альтернативными оценками, которые будут рассмотрены ниже.

2.2. Идентификация тренда медиан байесовских оценок интенсивности

В первую очередь отметим главный недостаток методологии AMFIT, свойственный всем частотным методам. По существу, в них производится подгонка центральных выборочных оценок nk/Ak к неизвестным истинным значениям интенсивности заболеваемости в стратах. Формально — это невыполнимая задача, поскольку ни одно истинное значение интенсивности заболеваемости не известно. Кроме того, совершенно непонятно, почему эмпирическая частотная оценка nk/Ak должна считаться центральной? О каком центре вообще идёт речь? Обычно в качестве центра некоторой случайной величины понимают одну из трех величин — моду, медиану или математическое ожидание. Для пуассоновского распределения (в произвольной страте) это Mo{n} = [h⋅A] (для нецелых произведений h⋅A), Me{n}≈h⋅A+1/3 и E{n}=h⋅A. При неизвестных h попасть ни в один из центров невозможно. Вся частотная теоретическая парадигма статистики строится на том, что за центр традиционно принимается математическое ожидание E{n} с оценкой в виде выборочного значения E{n}≈n_k. Но такой произвол никак не решает проблему оценивания центра показателя заболеваемости хотя бы потому, что h — непрерывная неизвестная величина, а её «центральные» частотные оценки nk/Ak дискретны в силу дискретности числителя.

Ослабить влияние двух отмеченных недостатков можно в рамках байесовского подхода к оценке центральных значений непрерывного показателя заболеваемости в страте при условии наблюдения имеющихся данных, если заменить распределение (1) сопряженным ему гамма-распределением

(3)

Его можно рассматривать как результат преобразования формулы (1) по теореме Байеса с учетом равновероятного доопытного ожидания любых интенсивностей h до проведения исследования (т.е. с учетом неинформативного приора). Разумеется, в качестве центра или центральной оценки в этом случае целесообразнее выбирать медиану, то есть точку, которая равновероятно удалена от концов области неопределенности всех возможных оценок. При этом, несмотря на интервальный подход в байесовском оценивании, идентификация центра — необходимая процедура, поскольку ставится задача определения кривой «доза — эффект», а не одной только доверительной полосы «доза — эффект». Мода распределения (3) совпадает с оценкой максимального правдоподобия (2) и эвристической частотной оценкой Mo{h Ak}=nk, что отчасти оправдывает процедуру построения функций правдоподобия и их оценки. Но в силу асимметрии (3) среднее уже сдвинуто на единицу в числителе E{h Ak}=nk+1. Для медианы аналогичной простой оценки не существует, но сдвиг относительно моды числителя монотонно убывает от значения ln(2) до 2/3 по мере увеличения числа случаев в страте. Для произвольного nk с успехом можно использовать аппроксимацию Me{h Ak}=μk≈2/3+0,205/(0,772+nk). Из соотношений следует, что эвристическая частотная оценка центра менее пригодна, чем математическое ожидание, но целесообразнее всё-таки воспользоваться модой. Эвристические частотные оценки дают систематическое занижение центральных оценок интенсивности. Оно меньше влияния случайного рассеяния, но при nk≤6 относительное смещение истинного центра достигает заметной величины до 10–100%, чем невозможно пренебречь. Для оценок же избытка относительного риска аналогичное смещение составит ещё бόльшую величину. В Таблице 1 таких страт 4 из 11. Оценка медиан интенсивностей имеет также важное свойство, характерное для отношений интенсивностей: медиана отношения (т.е. относительный риск) очень близка к отношению медиан гамма-распределений. Заметим, что такое свойство не выполняется для мод и математических ожиданий.

Производить вычисление тренда по всей таблице со стратифицированными точечными оценками по пуассоновскому функционалу Ω(β | Data) уже будет нельзя, так как требуется сохранить симметрию расположения краев доверительной области в пространстве параметров относительно вероятностного центра. Для этой цели лучше использовать взвешенный метод наименьших квадратов с известными дисперсиями по стратам. То есть функционал оценки принимаем в виде

(4)

где σ2h,k=[(nk+1)⋅(nk+2)-μ2k]/A2i — дисперсия распределения (3) относительно выбранного центра Me{hk} с обозначением μk=Me{h Ak =Ak⋅Me{hk}. Значения (4) вблизи минимума также можно приближенно рассматривать как случайные величины, распределенные по закону «хи-квадрат». Не останавливаясь подробно ни на процедуре минимизации, ни на анализе нулевой модели, приведем статистически значимый конечный результат. Он почти неизменен в оценке фоновой заболеваемости β0=26,9 (90% ДИ: 19,1 ... 34,7) на 10 000 человеко-лет. Оценка ERR/D = β1=0,786 (90% ДИ: 0,071 ... 1,50) (избыток риска на единицу дозы) увеличилась более, чем на 23%, что полностью соответствует коррекции числителя при рассмотрении центральных оценок за счет устранения систематического сдвига.

2.3. Байесовская оценка относительного риска при попарном сравнении страт

Использование распределений (3) для интервальных и центральных оценок позволяет выполнять также прямые (не косвенные) байесовские оценки относительного риска RR=RRk,0=hk/h0 для отношения двух случайных интенсивностей при попарном сравнении страт с номерами k и 0. Опираясь на законы преобразования распределений, можно заметить, что

(5)

В случае гамма-распределений этот интеграл берётся в элементарных функциях:

(6)

Более того, кумулятивная функция распределения относительного риска RR может быть представлена в виде регуляризованной неполной бета-функции Эйлера

(7)

что позволяет пользоваться практически любыми вычислительными программными продуктами, где эта функция табулирована. Исторически сложилось так, что первый аргумент неполной бета-функции называют параметром, а два значения nk+1 и n0+1 — переменными. Но в нашем случае смысл прямо противоположный, т.к. переменной в распределении (7) является относительный риск, а эмпирические данные играют роль фиксированных параметров.

В Таблице 2 приведены попарные оценки медиан относительного риска и оценки максимума правдоподобий, найденные численно по формулам (7) и (6). В последнем столбце вычислена величина Ibeta(Ak/(A0+Ak) | nk+1, n0+1), имеющая смысл односторонней оценки байесовского p-значения, как вероятности соответствия эмпирических данных гипотезе RRk,0<1, альтернативной предположению о повышенном риске при ненулевых дозах (для попарных сравнений).

Итоги применения трёх методов оценки риска удобно сопоставить на общем графике поведения величины избыточного относительного риска, как единообразной характеристики (рисунок 1). Без каких либо аналитических инструментов понятно, что не все методы приводят к близким результатам. Однако можно отметить, что регрессия байесовских медианных оценок интенсивности и прямые байесовские оценки медиан относительного риска почти воспроизводят друг друга, как этого и следовало ожидать. Вместе с тем и прямые максимально правдоподобные оценки относительного риска, и результаты косвенной пуассоновской регрессии по методу максимального правдоподобия AMFIT дают заметное отклонение от общего тренда. Более того, результаты для последних двух методов не совпадают. Основные отличия наблюдаются там, где число случаев в стратах мало.

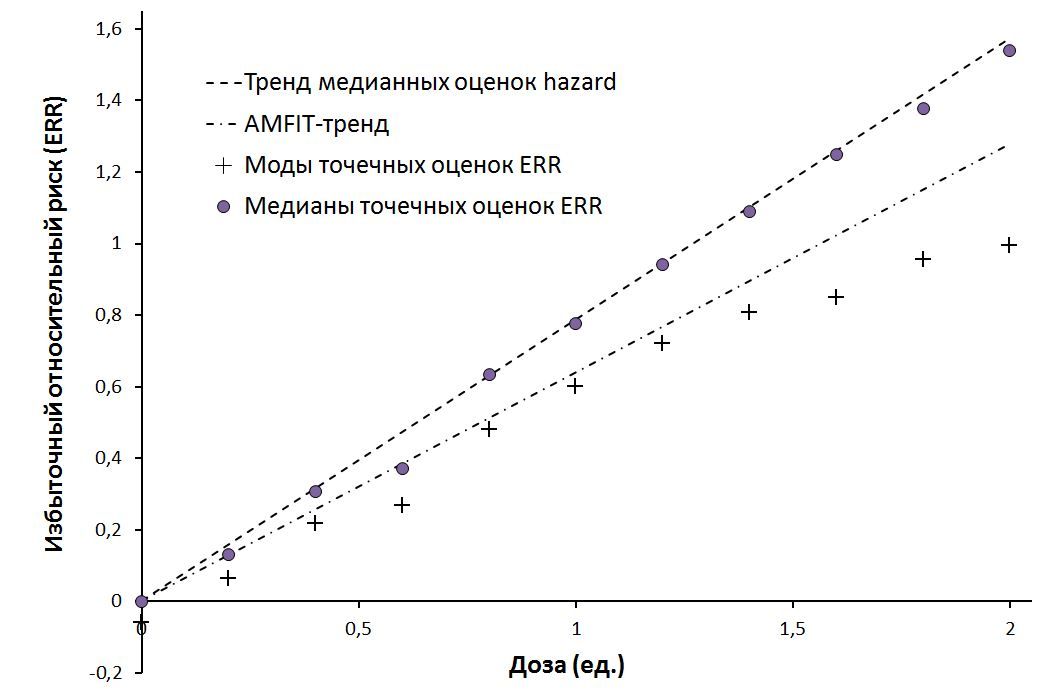
Рисунок 1 - Сводные результаты четырех методов оценки избыточного относительного риска

DOI:10.60797/jbg.2025.28.2.3

Причины такого поведения оценок ожидались (см. Введение), и наиболее просто понять их, обратив внимание на геометрические свойства плотности вероятности (3), имеющей существенно асимметричную форму. Скошенность приводит к тому, что положения моды, медианы и математического ожидания заметно расходятся, если число случаев в стратах n оказывается невелико. Однако сам принцип стратификации эпидемиологических наблюдений как раз и приводит к уменьшению числа случаев, а также к росту неопределенности оценок, усугубляющему возможное смещение. В таких условиях за центр доверительной области оценок интенсивности заболевания и относительного риска надёжнее принять медиану, а от принципа максимального правдоподобия (от оценок мод распределения) лучше отказаться.

Если принцип стратификации наблюдений в научной работе сохраняется, следует избегать ситуаций, приводящих к появлению страт с нулевыми или единичными наблюдениями случаев, т.к. это приводит к росту неконтролируемой относительной погрешности оценки интенсивностей или избыточных (над единицей) относительных рисков на десятки и даже сотни процентов, обессмысливая всё исследование. Иными словами, стратификация пространства факторов риска не может и не должна быть произвольно частой. Этого можно достичь, тщательно отсеивая малозначимые факторы риска и разумно подбирая границы страт в факторном пространстве. К сожалению, во многих исследованиях этому препятствует излишнее доверие к методам максимального правдоподобия и стремление учесть всевозможные факторы риска, включая фантастические.

В качестве экстремального подобного примера можно привести исследование риска смерти от почти всех возможных солидных злокачественных новообразований в Уральской когорте населения, спустя 40–70 лет после техногенного облучения в детском и юношеском возрасте. В работе

Другой негативный пример — публикация

Принятый в эпидемиологических исследованиях частотный (фишеровский) подход к количественному анализу стратифицированных наблюдений демонстрирует хорошую работоспособность только при большом количестве наблюдений, что не всегда доступно. Мощность исследований снижается также при наличии большого количества факторов риска и необходимости различать их по уровню влияния. Применение байесовского подхода к анализу наблюдений может несколько смягчить ограничения, поскольку он сочетает измерение со статистическим моделированием. В статье рассмотрено два таких алгоритма. Один сочетает байесовские оценки для страт с традиционными приёмами косвенной статистической регрессии, напоминающими алгоритм AMFIT. Другой — позволяет производить прямые интервальные и центральные оценки относительного риска при попарном сравнении страт с выбранной референтной группой. Оба алгоритма частично устраняют систематические искажения оценок риска, связанные с малым (n < 7) числом случаев в стратах, и приводят к сходным результатам, которые выглядят лучше, чем максимально правдоподобные частотные оценки. Оба алгоритма опираются на непрерывные распределения вероятности.