ОБ ОДНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАМОРАЖИВАНИЯ ЖИВОЙ БИОЛОГИЧЕСКОЙ ТКАНИ КРИОЗОНДОМ ЦИЛИНДРИЧЕСКОЙ ФОРМЫ

DOI: https:/doi.org/10.18454/jbg.2021.1.15.1

Buzdov B.K. *

Institute for Computer Science and Problems of Regional Management KBSC Russian Academy of Sciences, Nalchik, Russia

* Correspodning author (beslan.buzdov[at]yandex.ru, beslan2801[at]yandex.ru)

Received: 11.02.2021; Accepted: 20.04.2021; Published: 27.04.2021

ON ONE MATHEMATICAL MODEL OF FREEZING LIVING BIOLOGICAL TISSUE WITH A CYLINDRICAL CRYOPROBE

Research article

Abstract

When cooling living biological tissue (active, non-inert medium), cryoinstruments with various forms of cooling surface are used. Cryoinstruments can be located both on the surface of biological tissue, and completely penetrate into it. With a decrease in the temperature of the cooling surface, an unsteady temperature field appears in the tissue, which in the general case depends on three spatial coordinates and time. Of interest are both the distribution of the temperature field in the tissue, and the size of the zones of cryophase, freezing and the influence of cold, as well as the time of stabilization of the temperature field. Today there are a large number of scientific publications that consider mathematical models of cryodestruction of biological tissue. However, in the overwhelming majority of them, the Pennes equation (or some of its modifications) is taken as the basis of the mathematical model, from which the linear nature of the dependence of heat sources of biological tissue on the desired temperature field is visible. This character of the dependence does not allow one to describe the actually observed spatial localization of heat. In addition, Pennes' model does not take into account the fact that the freezing of the intercellular fluid occurs much earlier than the freezing of the intracellular fluid and the heat corresponding to these two processes is released at different times. In the proposed work, a new mathematical model of cooling and freezing of living biological tissue by a sufficiently extended cryoprobe with a cylindrical cooling surface is constructed. The model takes into account the above features and has applications in cryobiology and cryomedicine. A method is proposed for the numerical study of the problem posed, based on the application of the "through counting" technique without explicitly identifying the boundary of the influence of cold and the boundaries of the phase transition. The method was successfully tested earlier by the author in solving a number of twodimensional problems arising in cryomedicine. Some numerical computer calculations are presented.

Keywords: Mathematical modeling in cryobiology and criomedicine, spatial localization of heat, Stefan’s type problem.

Буздов Б.К. *

Институт информатики и проблем регионального развития Кабардино-Балкарского Научного Центра Российской Академии Наук (ИИПРУ КБНЦ РАН), Нальчик, Россия

* Корреспондирующий автора (beslan.buzdov[at]yandex.ru, beslan2801[at]yandex.ru)

Получена: 11.02.2021; Доработана: 20.04.2021; Опубликована: 27.04.2021

ОБ ОДНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАМОРАЖИВАНИЯ ЖИВОЙ БИОЛОГИЧЕСКОЙ ТКАНИ КРИОЗОНДОМ ЦИЛИНДРИЧЕСКОЙ ФОРМЫ

Научная статья

Аннотация

При охлаждении живой биологической ткани (активной, не инертной среды) используются криоинструменты с различными формами охлаждающей поверхности. Криоинструменты могут располагаться как на поверхности биоткани, так и полностью внедряться в нее. С понижением температуры охлаждающей поверхности в ткани возникает нестационарное температурное поле, зависящее в общем случае от трех пространственных координат и времени. Интерес представляют как распределение температурного поля в ткани, так и размеры зон криопоражения, замораживания и влияния холода, а также время выхода на стационар. На сегодняшний день существует большое количество научных публикаций, в которых рассматриваются математические модели криодеструкции биологической ткани. Однако, в подавляющем их большинстве за основу математической модели принимается уравнение Пеннеса (или некоторые его модификации), из которого виден линейный характер зависимости источников тепла биоткани от искомого температурного поля. Такой характер зависимости не позволяет описать реально наблюдаемую пространственную локализацию тепла. Кроме того, модель Пеннеса не учитывает того факта, что замерзание межклеточной жидкости происходит гораздо раньше, чем замерзание внутриклеточной жидкости и соответствующее этим двум процессам тепло выделяется в разные моменты времени. В предлагаемой работе построена новая математическая модель охлаждения и замораживания живой биологической ткани достаточно протяженным криозондом с цилиндрической формой охлаждающей поверхности. Модель учитывает указанные выше особенности и имеет приложение в криобиологии и криомедицине. Предложен метод численного исследования поставленной задачи, основанный на применении методики «сквозного счета» без явного выделения границы влияния холода и границ фазового перехода. Метод успешно опробован ранее автором при решении ряда двумерных задач, возникающих в криомедицине. Приведены некоторые численные расчеты на ЭВМ.

Ключевые слова: Математическое моделирование в криобиологии и криомедицине, пространственная локализация тепла, задачи типа Стефана.

1. Introduction

Lowering the temperature of biological tissues is widely used today for the preservation and storage of biomaterials - blood, bone marrow, individual organs, as well as in cryomedicine. The theoretical basis for the effect of low temperatures on biological objects is the physical processes of water freezing - the main component of the cellular structures of all living organisms. Thanks to the development of cryogenic technology, the method of cryotherapy has become widespread. Freezing living tissue, however, is significantly different from freezing water. The process of formation of ice crystals in living tissue almost always begins in the extracellular space with the appearance of crystallization centers and only after a significant decrease in temperature spreads into the cells. In order to turn the intercellular fluid into ice, it is necessary to reduce the temperature of the environment to -5 ° and below; to freeze the fluid inside the cells, a lower temperature is required (-20 ° and below). There is no comprehensive explanation of the mechanism of cold destruction of living cells and tissue. Numerous studies have made it possible to establish some of the reasons for the irreversibility of cell destruction during freezing. These factors include significant cell dehydration, leading to a sharp increase in the concentration of electrolytes, mechanical damage to cell membranes by ice crystals, as well as squeezing of cell bodies by these crystals, denaturation of phospholipids in cell membranes, cessation of intracellular fluid mobility, development of a focus of ischemic necrosis as a result of blood flow arrest in the volume of frozen tissue. The intensity of cryodestruction depends on the individual tissue resistance to cold, its temperature and cooling rate, exposure time, as well as the rate and time of tissue thawing after it. Cryoexposure is carried out using special devices, the main components of which are the tip of a directed and limited area of action, a reservoir with a refrigerant (autonomous devices) or a system of supply hoses that supply refrigerant to the tip from a stationary container. The most commonly used refrigerant is liquid nitrogen, nitrous oxide. There are also devices with a controlled freezing and thawing regime, capable of performing cryotherapy according to a pre-developed program and making adjustments to the process depending on the objective characteristics of tissue cooling. Depending on the nature of the problem, low temperatures are used in the range from -35 ° to -190 °; cold exposure varies considerably. Local cryogenic areas die off and are rejected by biological tissue, and the main task is to control cell death in a given volume. It is obvious that the development and introduction of the cryogenic method into wide practice largely depends on a reliable description of the thermal process of biological tissue freezing, accompanied by a water – ice phase transition. According to the dynamics of cryogenic damage (-20 ÷ -50° С) and freezing (0 ÷ -5° С) isotherms, the rate of temperature decrease, the time to reach a given or stationary state (exposure) and other parameters of cryogenic impact on biological tissue, it is possible to predict its results and simultaneously obtain the necessary data for calculating various cryoinstruments and equipment. In this regard, along with experimental studies, mathematical modeling of thermal processes in frozen biological tissue is relevant, requiring the development of effective methods for solving the Stefan problems arising here, a distinctive feature of which is the spatial localization of heat and the existence of stationary solutions. It should be noted that today there are a large number of scientific publications (see, for example, [1], [2], [3] and the literature cited there), in which mathematical models of cryodestruction of biological tissue are considered. However, in the overwhelming majority of them, the Pennes equation [4] is taken as the basis of the mathematical model, from which the linear character of the dependence of heat sources of biological tissue on the desired temperature field is seen. This character of the dependence fundamentally does not allow one to describe the actually observed spatial localization of heat. Local freezing and destruction of biological tissue is carried out by cryoinstruments with flat, cylindrical, hemispherical, spherical and other cooling surfaces located on the surface of biological tissue or embedded in it. With a decrease in temperature, an unsteady temperature field arises in the tissue. Damage to tissue cells occurs as a result of a phase change - freezing of biological tissue near the cooling surface. The propagation of the freezing front is prevented by the heat of crystallization released on it and the heat sources of blood and lymph flow, metabolism, and oxidative reactions acting in non-frozen tissue. This leads to the actually observed spatial localization of the thermal disturbance, and in the case of steady heat removal, to stabilization in time to the limiting spatially localized stationary state. At a specific temperature of the cryoinstrument, the freezing front spreads over the tissue to a certain limiting position. The corresponding limiting position of the cryogenic injury isotherm determines the maximum size of biological tissue destruction. The dynamics of cryogenic injury is influenced by the geometry of the cooling surface and its temperature, thermophysical characteristics of frozen and non-frozen tissue, blood temperature, blood flow rate in the tissue, and heat transfer conditions on the tissue surface.

2. Formulation of the problem

We will assume that the cryoinstrument has a cylindrical shape, is sufficiently extended and is completely embedded in biological tissue. Then the region in which we will seek the temperature distribution will have the shape of a ring. Due to the symmetry of the cryoinstrument, we obtain an initial-boundary value problem of the Stefan type, which has the form:

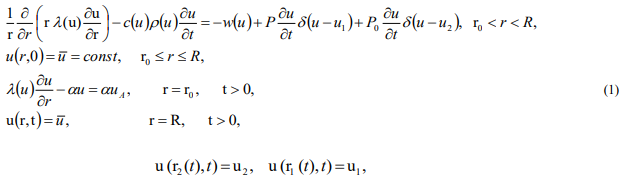
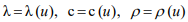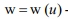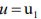Here  - the coefficients of thermal conductivity, heat capacity and density of biological tissue, respectively;  heat sources;  the coordinates of the freezing isotherm  and the cryogenic injury isotherm  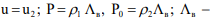the latent heat of crystallization of water;  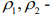arrays of extracellular and intracellular water per unit volume of biological tissue; 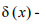Dirac function, initial temperature; - coefficient of heat transfer between the fabric and the cooling surface of the cryoinstrument; 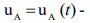temperature of the cooling surface of the cylindrical cryoprobe; 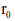– radius of cylindrical cryoinstrument;  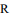– known constant characterizing the size of the considered area in which the problem is solved. The temperature field coordinates are to be determined.

3. Solution method

To solve the above problem (1), we choose the method described in [8], [9], based on preliminary smoothing of the coefficients. Note that the functions 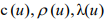 have a discontinuity of the first kind at the points  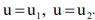In the remaining parts of the domain of definition, we will assume that they are sufficiently smooth. Let's introduce the specific heat content.

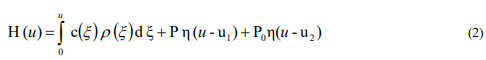
Here 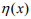 is the Heaviside function. Direct application of difference schemes to the problem at hand does not give practically good results. To make the use of difference schemes more efficient, it is expedient to subject the functions  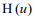and 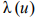 to smoothing (in the present work, zero-order smoothing was used [10]). After smoothing the discontinuous functions, we differentiate the smoothed function  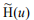and obtain the boundary value problem (3), the solution of which, under certain requirements for the given functions and smoothing, tends [8] to the solution of problem (1):

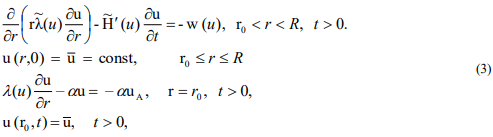
Solving approximately the boundary value problem (3), we thereby obtain an approximate solution to the problem (1). Numerical experiments show that it is convenient to use an implicit difference scheme for this purpose. For ensuring spatial localization of heat, nonlinear function of heat sources has to satisfy to the certain properties described in [5]. In computer simulation in this paper we considered power dependence

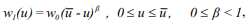 logarithmic dependence of heat source from temperature  and dependence

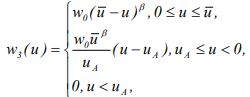
The simulations were performed for the following values of thermophysical properties of biological tissue.

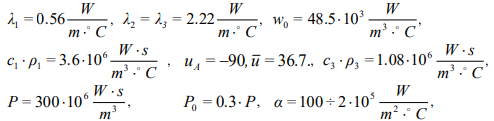
Indexes 1, 2, 3 refer to the chilled, frozen and affected by cryodestruction areas of biotissue respectively. Comparison of the results shows a similar character of dynamics for freezing and cryodestruction isotherms for all three types of heat sources. Note that the second functional dependency contains only one experimentally determined parameter.

4. Difference scheme

Let us introduce a grid on 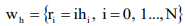 a segment  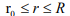and a grid  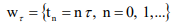with a step  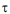on a segment  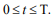Here 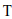 is a certain moment in time, up to which the development of the heat propagation process of interest to us is considered. In this work, the following purely implicit scheme was used to solve problem (4):

 

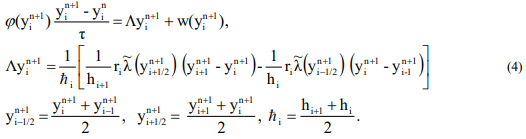
Introduced designation: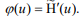

A nonlinear relatively 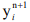 three-point equation must be solved by some iterative method (for example, Newton's method), and each of the iterations can be found by the sweep formulas. The boundary conditions corresponding to equation (4) will be as follows:

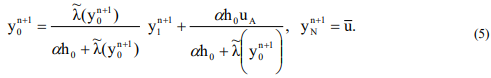
Thus, we obtained scheme (4), (5), according to which all the calculations necessary for solving problem (1) were subsequently carried out. It should be noted that when determining 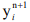 by the iteration method, the coefficients  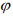and 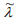 can be taken at the previous iteration [10].

5. Results of computer simulation

Following are some thoughts about results obtained for those problems:

1). results are quite consistent with the results obtained for other two-dimensional problems considered earlier by the author, as well as with the results obtained by other authors [6], [7] when considering the one-dimensional non-stationary Stefan’s type problems arising in cryosurgery;

2). the effect of spatial localization of heat enables to pass from problem for an unbounded domain to problem for a domain with the known boundaries;

3). analysis of the calculations made it possible to trace stabilization of the temperature field and the field of isotherms to the ultimate steady state;

4). an association between the steps in time and space is found, which means that the difference schemes are conditionally stable;

5). under initial data 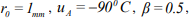following results were found: stabilization to limiting steady state is reached after about 6 minutes, radius of the affected area is around 14 mm, radius of freezing biotissue zone 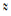17 mm, radius of cooled biotissue zone 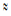30 mm.

6. Discussion

Summing up, the following are most important aspects of Stefan’s type problems arising in cryobiology:

1) One of the most important features of the abovementioned Stefan’s type problems is actually observed effect of spatial localization of heat, which is associated with the presence of nonlinear biological heat sources of a special kind. Although this effect complicates the mathematical model (a nonlinear term, depended on the desired temperature field, appears in equation), it also allows to move from statements of problems in an unbounded domain to problems in bounded domain.

2) Nonlinear heat sources depend on the numerical parameters that must be determined experimentally. This is an additional and quite complicated task.

3) The methodology of computation with preliminary smoothing of discontinuous functions is independent of the dimension of the problem and can be used without any change for solving two and three-dimensional problems.

4) The link between the steps in time and space, found in the simulations, shows that the constructed difference schemes are conditionally stable.

Other works of the author of the article on the proposed topic can be viewed in [11], [12], [13], [14], [15], [16], [17].

Conflict of Interest

None declared.

Конфликт интересов

Не указан.