A NOVEL ROLLING BASED DNA CRYPTOGRAPHY

1. Introduction

Cryptography is the art of Data hiding. This is often considered as the primary defense of data privacy. Cryptography using DNA sequence is a new approach. Here DNA sequence is used as the key and encrypted data also a sequence of DNA. It is very useful, as the key length has no limitation so the security is better and with proper encryption algorithm it can defend many attacks. In this paper we introduced a new approach of DNA based cryptography. We described our approach here step by step with proper example and implementation and security analysis is also given here.

2. Methods

The process can be divided into two steps.

2.1. Encryption

The whole encryption process is done in five steps. They are.

1. Key Analysis
2. Data and Key Arrangement
3. Roll in encoding
4. Secondary Arrangement
5. Shifting

2.1.1. Key analysis

First we need to calculate the key size. Key size depends on binary data size. If the binary data has n bit then key size is n/2. Key size varies data to data so key are generated and used as one time pad. Key size can be very large or very small so there is no limitation for same size different key. Once the key is generated then the frequencies of DNA base A, T, C and G are calculated. The frequency of A, T, C, G define the level and order for the next steps.

2.1.2. Data and Key arrangement

In first step we calculated the frequency of A, T, C and G. Now use that information for Data and Key arrangement. The frequency of A defines the level of arrangement for Data. The term level of arrangement for data refers that how many times A or V order arrangement will be applied on the data. For example if frequency of A is 17 then the level of arrangement for data is 17. That is mean A order arrangement is applied 17 times on data and order of arrangement is A as frequency of A is odd number. Similarly level of arrangement for key refers that how many times A or V order will be applied on the key. For key arrangement, Level is equal to frequency of T and similarly order is A if frequency of T is Odd and V if frequency of T is Even. The order of A and V is given below:

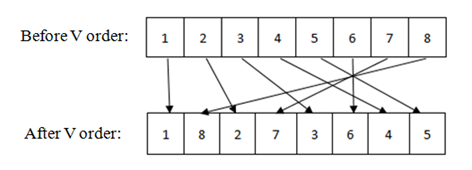
Fig. 1 - V-order

Here in fig. we see before we apply V order the bit positions is 1,2,3,4,5,6,7,8 After we apply V order then bit position is 1,8,2,7,3,6,4,5 It mixed leftmost and rightmost bit together. To do that it take leftmost bit and then place rightmost bit next to it of the data, then again leftmost and then rightmost bit from rest of the bits and continue it until end. A order is also a special sequence of bit position of a data. Here A order is given:

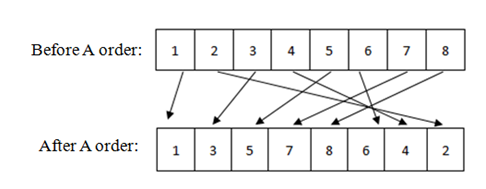
Fig. 2 - A-order

Here in Figure 1 we see before A order is applied, the sequence of data is 1,2,3,4,5,6,7,8 and after A order is applied, the sequence of data is 1,3,5,7,8,6,4,2. Here the first half is filled with odd bit position from left to right and then even bit position from right to left. There is a relation between A order and V order. To get unordered or original data from an A-ordered data we need to apply V order on that A ordered data and to get unordered data from a V-ordered data we need to apply A order on that V ordered data.

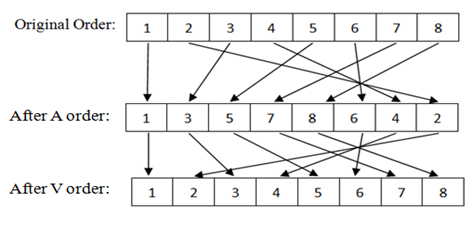
Fig. 3 - Relation of A-order and V-order

2.1.3. Roll in encoding

After the Data and Key ordered in the calculated order and level according to the frequency of A and T now both are encoded in a process called ‘Roll-in’ (Clock wise rotation).

Fig. 4 - Roll in encoding

In this process 2bit binary data is used as a binary value. So it can be 01,00,10 or 11 in decimal 0,1,2 or 3. Now this 2 bit binary value defines the rotation position for the key bit. Here 1 bit key and 2 bit data is encoded to produce 1bit Rolled-in data. For example if binary 2 bit is 01 that’s mean 1 in decimal and corresponding key bit is A then a is rotated in clock wise one position and produce 1 bit Rolled-in data that is T (from the given figure). Similarly if the data bit value is 11 and key bit is C then the Rolled-in data bit is T.

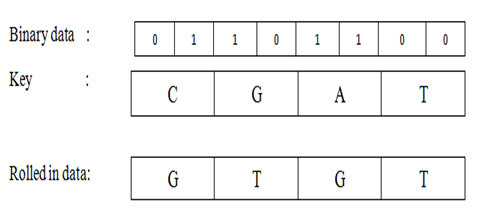
Fig. 5 - Rolled in data

2.1.4. Secondary arrangement

After produced the Rolled-in Data the next step is secondary arrangement. This is similar with the previous Data and Key arrangement. Here the frequency of C is used to calculate the order and level for the rolled-in data. The Rolled-in data is arranged according to order and level and produced secondary arranged data.

2.1.5. Shifting

This is the final step for this encryption process. The frequency of G is used to calculate the shift position. For example if the frequency of G is 17 then the secondary arranged data is shifted 17 bit left.

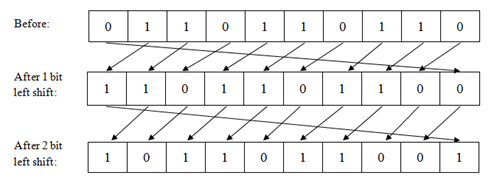
Fig. 6 - Shifting (left-shift)

After this step we get the final encrypted data. Now we can send it via public network and send the original key via private network

2.2. Decryption

The Decryption process has six main steps. They are mostly similar with the steps of encryption but there is difference in their order. Those steps are:

1. Key Analysis
2. Shifting
3. Secondary Arrangement
4. Key Arrangement
5. Roll-out decoding
6. Data Arrangement

2.2.1. Key analysis

This is the same step that is used in encryption process. In this step we calculate the frequency of A, T, C and G from given key.

2.2.2. Shifting

After calculating the frequency of the DNA base from the key, we use the frequency of G to shift the encrypted data. This time we shift the encrypted data G bit right so that we can get the actual secondary arranged data as we know the secondary arranged data shift G bit left.

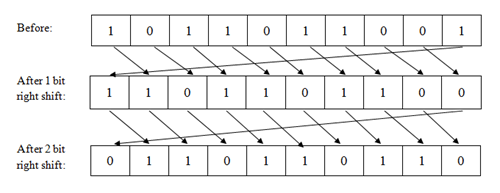
Fig. 7 - Shifting (right shift)

2.2.3. Secondary arrangement

We have now secondary arranged data so now we use the frequency of C to get the Rolled-in data. To do that, we calculate the order and level. Level is the same as the frequency of C and the order is V if frequency is Even number and order is A if the frequency of C is Odd. We know A and V order are reverse to each other so if the calculation define the order is A then we arrange the secondary arranged data in V order in frequency of C times to get the actual Rolled-in data. If the calculated order is V then similarly we arrange the secondary arranged data in A order in the frequency of C times to get the actual Rolled-in data.

2.2.4. Key arrangement

Now we need to arrange the key according to the frequency of T. If the frequency of T is Even the order is V or if the frequency of T is Odd then the order is A and the level is the same as the frequency of T. This is same as encryption process step data and key arrangement.

2.2.5. Roll out decoding

This Roll-out decoding is the reverse process of roll-in encoding. Here rolled-in data that we get from secondary arrangement step and arranged key from key arrangement step used as input and produce binary data. This is anti clockwise rotation process.

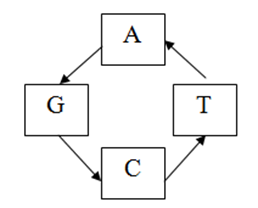
Fig. 8 - Roll-out Decoding

Here we take 1 bit rolled-in data and 1 bit arranged key then we rotate anti clockwise until both data bit match. Here start position is the key bit. That’s mean we need to consider rolled-in data bit fixed and rotate the key bit in anti clock wise direction. If we have to move 2 positions to match them then the binary data is 10, that is the binary value of 2. For example if the rolled-in data bit is G and arranged key bit is C then to match them we need to move C, 1 bit to get G in anti clock wise direction. So the binary value is 10. So we get 2-bit binary value from 1 bit rolled-in data. After this step we get the arranged binary data.

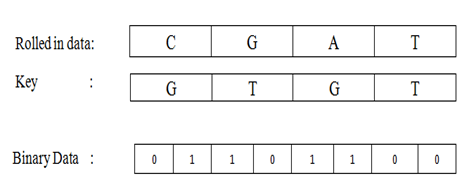
Fig. 9 -Roll-out data

2.2.6. Data arrangement

After Roll-out decoding we gain the arranged binary data. So now we have to rearrange the binary data. To do that we need to calculate order and level from the frequency of A. Level is the same as the frequency of A and the order is V if frequency is Even number and order is A if the frequency of A is Odd. We know A and V order are reverse to each other so if the calculation define the order is A then we arrange the arranged binary data in V order in frequency of A times to get the actual binary data. If the calculated order is V then similarly we arrange the arranged binary data in A order in the frequency of A times to get the actual binary data.

3. Example

We illustrate the encoding and decoding with an example. We use the same example for encryption and decryption. For example we use a massage, "This is year 2017". Now we will show the encryption and decryption process with this example.

3.1. Encryption

In Binary the data is :

01010100011010000110100101110011001000000110100101110011001000000111100101100101011000010111001000
10000000110010001100000011000100110111

So the binary data size 136. So key size is (136/2) = 68.

Here we use the following as key:

CGGTGATGTTAACATAGATTCGGCACATTACTCTTGTAGGTGTGGAATCACTTAGCTACGCGGCGAAG

3.1.1. Key analysis

Here,

Frequency of A is: 17

So the data arrangement level is: 17 and

17 is odd data arrangement order is: A

Frequency of T is: 19

So the key arrangement level is: 19 and

19 is odd data arrangement order is: A

Frequency of C is: 13

So the secondary arrangement Level is: 13 and

13 is odd secondary arrangement Order is: A

Frequency of G is: 19

So secondary arranged data will shift 19 bit left.

3.1.2. Data and Key arrangement

Now we arrange the data and the key.

Data (before arrangement):

01010100011010000110100101110011001000000110100101110011001000000111100101100
10101100001011100100010000000110010001100000011000100110111

Data (After arrangement):

0011011010101011001100100010111001000011100010010000101110000100111011000000
101101101000110000010011000100001100011000001001100110001110

Key (Before Arrangement):

CGGTGATGTTAACATAGATTCGGCACATTACTCTTGTAGGTGTGGAATCACTTAGCTACGCGGCGAAG

Key (After Arrangement):

CTTGGATGACCCTGACGGTGTCGTTCGGACCTGGAATTATCTAGGAGTAAGCGTTCCTAAAGGTTAAA

3.1.3. Roll in encoding

Here we show the roll in encoding on the arranged data.

Arranged data:

00110110101010110011001000101110010000111000100100001011100001001110110000001011011010
00110000010011000100001100011000001001100110001110

Arranged Key:

CTTGGATGACCCTGACGGTGTCGTTCGGACCTGGAATTATCTAGGAGTAAGCGTTCCTAAAGGTTAAA

Rolled-in Data:

CACTTCGCATCATTGAAGTCGCTCTCTCCCGTCTGATTCAGGCGCAGCAGGGGTACGGAACATCGAGC

3.1.4. Secondary arrangement

The secondary arrangement is applied on the rolled in data in this step.

Rolled-in Data:

CACTTCGCATCATTGAAGTCGCTCTCTCCCGTCTGATTCAGGCGCAGCAGGGGTACGGAACATCGAGC

Secondary Arranged Data:

CGGGTCTTATCCTCTGTGTCGCACACCAACCGTGCGCCGGAAGGCACTATCTAACATCGCAAGTGGTG

3.1.5. Shifting

We shift left the secondary arranged data in this step. The shifted data is transmitted to toe receiver.

Secondary Arranged Data:

CGGGTCTTATCCTCTGTGTCGCACACCAACCGTGCGCCGGAAGGCACTATCTAACATCGCAAGTGGTG

Shifted Data (Final Encrypted Data):

CGCACACCAACCGTGCGCCGGAAGGCACTATCTAACATCGCAAGTGGTGCGGGTCTTATCCTCTGTGT

3.2. Decryption

After receiving the encrypted data the receiver decrypts the data using the same key.

Encrypted Data:

CGCACACCAACCGTGCGCCGGAAGGCACTATCTAACATCGCAAGTGGTGCGGGTCTTATCCTCTGTGT

Key:

CGGTGATGTTAACATAGATTCGGCACATTACTCTTGTAGGTGTGGAATCACTTAGCTACGCGGCGAAG

3.2.1. Key analysis

This is the same step that is used in encryption process.

Frequency of A is: 17

So the data arrangement level is: 17 and

17 is odd data arrangement order is: V (reverse of A)

Frequency of T is: 19

So the key arrangement level is: 19 and

19 is odd data arrange order is: A

Frequency of C is: 13

So the secondary arrangement level is: 13 and

13 is odd secondary arrangement order is: V (reverse of A)

Frequency of G is: 19

So secondary arranged data will shift 19 bit right.

3.2.2. Shifting

The reverse shift of encryption is applied to the encrypted data.

Encrypted Data:

CGCACACCAACCGTGCGCCGGAAGGCACTATCTAACATCGCAAGTGGTGCGGGTCTTATCCTCTGTGT

Secondary Arranged Data (After Right Shift):

CGGGTCTTATCCTCTGTGTCGCACACCAACCGTGCGCCGGAAGGCACTATCTAACATCGCAAGTGGTG

3.2.3. Secondary Arrangement

After shifting right shift) we get secondary arranged data. Now we rearrange it to get Rolled-in data. To do that, we need to use reverse order in same level. In this case we use V order as it was arranged in A order.

Secondary Arranged Data:

CGGGTCTTATCCTCTGTGTCGCACACCAACCGTGCGCCGGAAGGCACTATCTAACATCGCAAGTGGTG

 Rolled-in Data (After Secondary Arrangement):

CACTTCGCATCATTGAAGTCGCTCTCTCCCGTCTGATTCAGGCGCAGCAGGGGTACGGAACATCGAGC

3.2.4. Key Arrangement

Now we arrange the key in same format as in encryption process.

Key (Before Arrangement):

CGGTGATGTTAACATAGATTCGGCACATTACTCTTGTAGGTGTGGAATCACTTAGCTACGCGGCGAAG

Key (After Arrangement):

CTTGGATGACCCTGACGGTGTCGTTCGGACCTGGAATTATCTAGGAGTAAGCGTTCCTAAAGGTTAAA

3.2.5. Roll-out Decoding

Now we have arranged key and rolled out data. With the help of Roll-out decoding arranged binary data can be gained.

Rolled-in Data:

CACTTCGCATCATTGAAGTCGCTCTCTCCCGTCTGATTCAGGCGCAGCAGGGGTACGGAACATCGAGC

Arranged Key:

CTTGGATGACCCTGACGGTGTCGTTCGGACCTGGAATTATCTAGGAGTAAGCGTTCCTAAAGGTTAAA

Arranged Data: (After Roll-out Decoding)

00110110101010110011001000101110010000111000100100001011100001001110110000001011011010
00110000010011000100001100011000001001100110001110

3.2.6. Data Arrangement

Now we have data but it is arranged according to frequency of A .Now we rearranged it in V (for this case as we applied A order for arranging) order to get original data.

Arranged Data:

00110110101010110011001000101110010000111000100100001011100001001110110000001011011010001100000
10011000100001100011000001001100110001110

Original Data (After V-order in this case):

0101010001101000011010010111001100100000011010010111001100100000011110010110010101100001011100
100010000000110010001100000011000100110111

Now we get the original binary data that represent original massage "This is year 2017".  

4. Results

We analyzed the performance of this method in terms of security.

• In this cryptography we use frequency of the DNA base of the key so 1 bit change can affect on whole data so even 99.99% matched key can’t reveal any part of the original data. For example here is a situation where same encrypted data is decrypted with original key, 3bit mismatched key, 2bit-mismatched key and only 1bit mismatched key and the result is showed. First original key is used:

Fig.10 - Result of original key

Now first three bit of the key is changed.

Fig.11- Result of 3bit change in key

Now last two bit is different of the key.

Fig.12- Result of 2bit changed key

Now only one bit change in first and last position of the key.

(a) Encrypted data using original key

(b) Encrypted data using changed key

Fig.13 - Result of 1bit change in key in first and last position

So as we see here only one bit mismatched can affect in whole data. So to break this pure key is needed. Without 100% matched key no data can be gain.

• Here as the key size depends on data size and the length of key is normally so we use key as one time pad as there is enough available key for the long length data. So we can get the benefit of one time pad in this cryptography.
• We use one time pad key here. That’s why known plaintext analysis is not effective for this cryptography.
• We use roll-in encoding that produce output according to the data bit so frequency analysis is not possible for this cryptography. Here a sample result of frequency analysis is given where same key with different data is used to produce encrypted data.

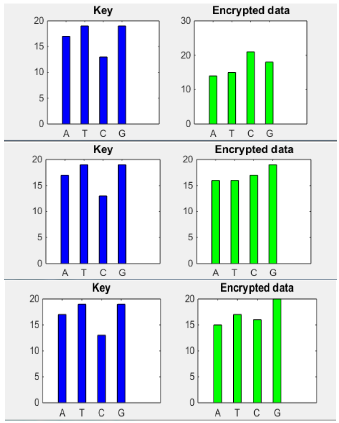
Fig.14 - Frequency analysis of key and encrypted data

Here frequency analysis results show that encrypted data frequency totally different from each other while key is same for all of them. It shows that there is no relation between key and encrypted data so key prediction from encrypted data is not possible.

• Brute force is very time consuming for this cryptography as key length is normally very large and almost same key does not reveal any part of real data so this is not a good crypto analysis for this algorithm.

5. Conclusion

In this paper we proposed a new algorithm for DNA cryptography. Here we include some features of dynamic value for encrypted data that make it harder to predict key from encrypted data, relatively small encrypted data size without compromising security that save memory space, sensitivity to frequency of DNA base of the key that ensure that only proper key can reveal the original data. There is a future working scope with this algorithm to reduce its complexity and make a simplified key generation method. With further study we can overcome those for better performance.