APPLICATIONS OF SOME NEW TRANSMUTED CUMULATIVE DISTRIBUTION FUNCTIONS IN POPULATION DYNAMICS
APPLICATIONS OF SOME NEW TRANSMUTED CUMULATIVE DISTRIBUTION FUNCTIONS IN POPULATION DYNAMICS
Funding
This work has been supported by the project FP17-FMI-008 of Department for Scientific Research, Paisii Hilendarski University of Plovdiv.
Conflict of Interest
None declared.
Vesselin Kyurkchiev1, Anton Iliev1,2*, Nikolay Kyurkchiev1
1Faculty of Mathematics and Informatics, University of Plovdiv Paisii Hilendarski,
24, Tzar Asen Str., 4000 Plovdiv, Bulgaria
2Institute of Mathematics and Informatics, Bulgarian Academy of Sciences,
Acad. G. Bonchev Str., Bl. 8, 1113 Sofia, Bulgaria
*To whom correspondence should be addressed.
Associate editor: Giancarlo Castellano
Received on 02 April 2017, revised on 10 April 2017, accepted on 25 April 2017.
Abstract
Motivation: In literature, several transformations exists to obtain a new cumulative distribution function (cdf) using other(s) well-known cdf(s).
Results: In this note we find applications of some new cumulative distribution function transformations to construct a family of sigmoidal functions based on the Verhulst logistic function.
We prove estimates for the Hausdorff approximation of the shifted Heaviside step function by means of this family. Numerical examples, illustrating our results are given.
Keywords: Cumulative Distribution Function, Logistic Function, Shifted Heaviside Step Function, Hausdorff Distance, Upper and Lower Bounds.
Contact: aii@uni-plovdiv.b
1. Introduction
In literature, several transformations exists to obtain a new cumulative distribution function (cdf) using other(s) well-known cdf(s) (Aryal & Tsokos, 2009; Aryal, 2013; Gupta, R. G., Gupta, P. L. & Gupta, R. D., 1998; Khan & King, 2013; Kumar, Singh, & Singh, 2015a; Kumar, Singh & Singh, 2015b; Kumar, Singh & Singh 2017).
Definition 1 Another popular transformation by using a (cdf) F(t) is (Kumar, Singh, & Singh, 2015a):
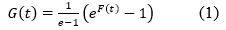
The transformation (1) has great applications in data analysis.
Definition 2 Define the logistic (Verhulst) function f on R as
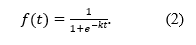
The logistic function belongs to the important class of smooth sigmoidal functions arising from population and cell growth models.
Since then the logistic function finds applications in many scientific fields, including biology, population dynamics, chemistry, demography, economics, geoscience, mathematical psychology, probability, financial mathematics, statistics, insurance mathematics to name a few (Anguelov & Markov, 2016; Lente, 2015; Kyurkchiev & Markov, 2016a; Kyurkchiev, 2016a; Costarelli & Spigler, 2013; Kyurkchiev & Markov, 2014; Kyurkchiev & Markov, 2015; Kyurkchiev & Markov, 2016b).
Definition 3 The (interval) step function is:
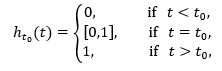
usually known as shifted Heaviside step function.
Definition 4 (Hausdorff, 2005; Sendov, 1990) The Hausdorff distance (the H–distance) ρ(f,g) between two interval functions f,g on Ω⊆R, is the distance between their completed graphs F(f) and F(g) considered as closed subsets of Ω×R. More precisely,
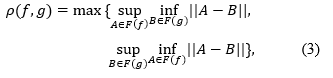
wherein ||.|| is any norm in R2, e. g. the maximum norm ||(t,x)||=max{|t|,|x|}; hence the distance between the points A=(tA,xA), B=(tB,xB) in R2 is ||A-B||= max (|tA-tB|,|xA-xB|).
In this paper we discuss several computational, modelling and approximation issues related to two familiar classes of sigmoidal functions–these are the families of transmuted cumulative distribution functions.
2. Methods
1. Let us consider the following sigmoid
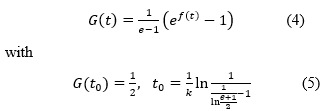
based on (1) with the Verhulst logistic function f(t).
The one–sided H-distance d=ρ(ht0,G) between the shifted Heaviside step function ht0 and the sigmoidal function G satisfies the relation:
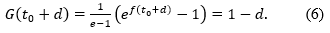
The following theorem gives upper and lower bounds for d=d(k).
Theorem 2.1 The one–sided H-distance d(k) between the function ht0 and the function G can be expressed in terms of the rate parameter k for any real k≥2 as follows:
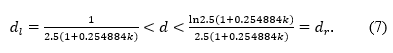
Proof. We define the functions
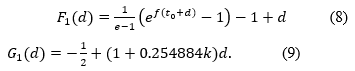
From Taylor expansion
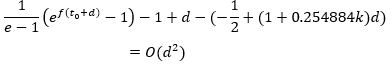
we see that the function G1(d) approximates F1(d) with d→0 as O(d2) (see Figure 1).
In addition G'1d>0 and for k≥2.
G1(dl)<0; G1(dr)>0.
This completes the proof of the inequalities (7).
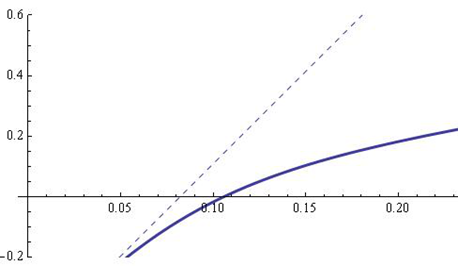
Fig. 1 - The functions  and
and  for
for 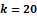 .
.
The generated sigmoidal function G(t) for k=20 is visualized on Figure 2.
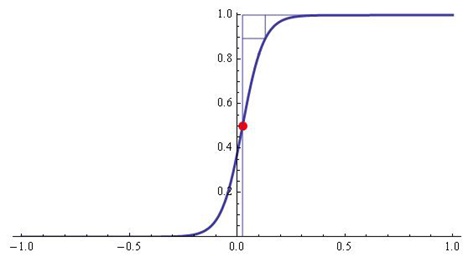
Fig. 2 - The H-distance d(k) between the functions 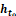 and G for k=20 is d=0.105561;
and G for k=20 is d=0.105561;  ;
; 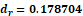 .
.
Some computational examples using relations (7) are presented in Table 1. The third column of Table 1 contains the value of d for prescribed values of k computed by solving the nonlinear equation (6).
Table 1. Bounds for d(k) computed by (6) and (7) for various rates k
|
k |
dl |
d computed by (6) |
dr |
|
30 |
0.0462014 |
0.0747728 |
0.142182 |
|
40 |
0.0357291 |
0.0627923 |
0.119042 |
|
50 |
0.0291032 |
0.0541761 |
0.102935 |
|
100 |
0.015101 |
0.0296749 |
0.0633183 |
|
500 |
0.00311425 |
0.00617859 |
0.0179747 |
|
1000 |
0.00156321 |
0.0048109 |
0.0100999 |
Definition 5 Another popular transformation by using a (cdf) F(t) is (Kumar, Singh & Singh, 2017):
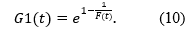
2. Let us consider the following sigmoid
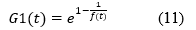
with
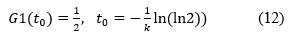
based on (10) with the Verhulst logistic function f(t).
The one–sided H-distance 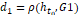 between the shifted Heaviside step function
between the shifted Heaviside step function 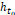 and the sigmoidal function G1 satisfies the relation:
and the sigmoidal function G1 satisfies the relation:
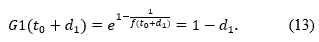
The following theorem gives upper and lower bounds for 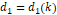
Theorem 2.2 The one–sided H-distance 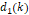 between the function
between the function 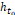 and the function
and the function 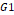 can be expressed in terms of the rate parameter
can be expressed in terms of the rate parameter 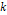 for any real
for any real 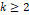 as follows:
as follows:
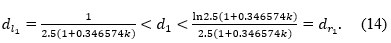
The proof follows the ideas given in this paper and will be omitted.
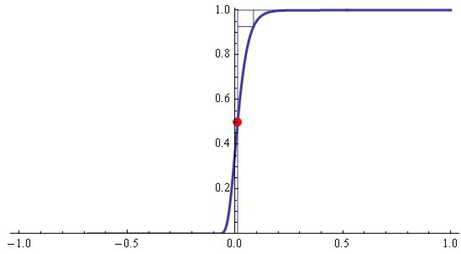
Fig. 3 - The H-distance 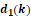 between the functions
between the functions 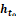 and
and 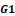 for
for 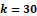 is
is 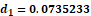 .
.
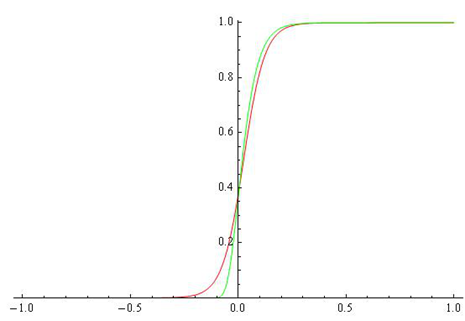
Fig. 4 - Comparison between G (red) and G1 (green) for k=20.
3. Results
To achieve our goal, we obtain new estimates for the one–sided H-distance between a shifted Heaviside step function and its best approximating family of transmuted cumulative distribution functions–these are the families of functions G(t) and G1(t) based on the Verhulst logistic function.
Numerical examples, illustrating our results are given.
In some cases the approximation of shifted Heaviside function by G1(t) is better in comparison to its approximation by G(t) (see Figure 4).
For other results, see (Iliev, Kyurkchiev & Markov, 2017a; Kyurkchiev, 2015; Kyurkchiev & Iliev, 2016; Kyurkchiev, V. & Kyurkchiev, N., 2015; Kyurkchiev & Markov, 2016c; Iliev, Kyurkchiev & Markov, 2017b; Kyurkchiev, V. & Kyurkchiev N., 2017; Kyurkchiev, 2016b).
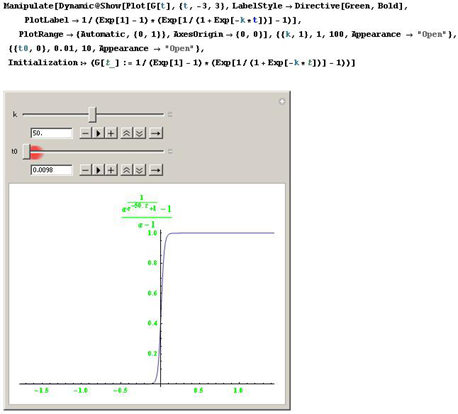
Fig. 5 - Software tools in CAS Mathematica.
We propose a software module within the programming environment CAS Mathematica for the analysis of the considered families of transmuted cumulative distribution functions.
The module offers the following possibilities:
- generation of the functions G(t) and G1(t) under user defined values of the reaction rate k and t0;
- calculation of the H-distance between the Heaviside function ht0 and the sigmoidal functions G(t) and G1(t);
- software tools for animation and visualization.
4. Appendix
Focusing on the shifted logistic function
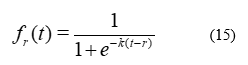
and the shifted function
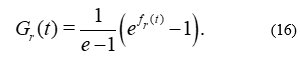
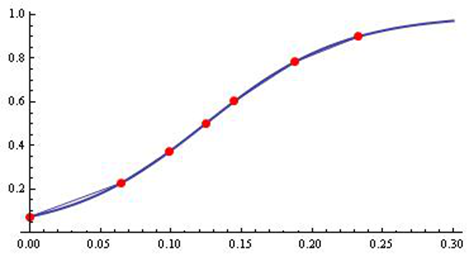
Fig. 6 - Interpolation of the experimental data by model (16).
We examine the following experimental data (biomass) for Xantobacter autotrophycum by the model 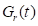 .
.
Table 2. The experimental data (biomass) for Xantobacter autotrophycum and approximation by 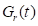 for
for 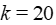 and
and 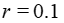
|
|
Biomass |
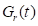 |
|
0 |
0.104 |
0.0736774 |
|
0.065 |
0.233 |
0.229003 |
|
0.099 |
0.39 |
0.372755 |
|
0.125 |
0.507 |
0.50254 |
|
0.145 |
0.618 |
0.602883 |
|
0.188 |
0.766 |
0.784021 |
|
0.233 |
0.88 |
0.899886 |
From Figure 6 it can be seen that the results are satisfactory. We point out that in similar ”exponential” data type the results are near to Gompertz growth model.
Acknowledgment. The authors would like to thank the anonymous reviewers for their valuable comments and suggestions to improve the paper quality.
References
Anguelov, R. & Markov, S. (2016). Hausdorff Continu-ous Interval Functions and Approximations, In: M. Nehmeier et al. (Eds), Scientific Computing, Computer Arithmetic, and Validated Numerics, 16th International Symposium, SCAN 2014, LNCS 9553, 3-13, Springer. doi:10.1007/978-3-319-31769-4
Aryal, G. R. (2013). Transmuted log-logistic distribution. Journal of Statistics Applications and Probability, 2 (1), 11-20.
Aryal, G. R. & Tsokos, C. P. (2009). On the transmuted extreme value distribution with application, Nonlinear Analysis: Theory, Methods and Applications, 71 (12), 1401-1407.
Costarelli, D. & Spigler, R. (2013). Constructive Ap-proximation by Superposition of Sigmoidal Functions. Analysis in Theory and Applications, 29 (2), 169-196. doi:10.4208/ata.2013.v29.n2.8
Gupta, R. G., Gupta, P. L. & Gupta, R. D. (1998). Mod-eling failure time data by Lehman alternatives. Communica-tions in Statistics, Theory and Methods, 27, 887-904.
Hausdorff, F. (2005). Set Theory (2 ed.), Chelsea Pub-lishing, New York, Republished by AMS-Chelsea.
Iliev, A., Kyurkchiev, N. & Markov, S. (2017a). On the Approximation of the step function by some sigmoid func-tions. Mathematics and Computers in Simulation, 133, 223-234. doi:10.1016/j.matcom.2015.11.005
Iliev, A., Kyurkchiev, N. & Markov, S. (2017b). A fami-ly of recurrence generated parametric activation functions with applications to neural networks. International Journal on Research Innovations in Engineering Science and Tech-nology (IJRIEST), 2 (1), 60-68.
Khan, M. & King, R. (2013). Transmuted modified Weibull distribution: A generalization of the modified Weibull probability distribution. European Journal of Pure and Applied Mathematics, 6 (1), 66-88.
Kumar, D., Singh, U. & Singh, S. (2015a). A method of proposing new distribution and its application to Bladder cancer patients data. Journal of Statistics Applications & Probability Letters, 2 (3), 235-245.
Kumar, D., Singh, U. & Singh, S. (2015b). A new distri-bution using sine function and its application to Bladder cancer patients data. Journal of Statistics Applications & Probability, 4 (3), 417-427.
Kumar, D., Singh, U. & Singh, S. (2017). Lifetime dis-tribution: derived from some minimum guarantee distribu-tion. Sohag Journal of Mathematics, 4 (1), 7-11.
Kyurkchiev, N. (2015). On the Approximation of the step function by some cumulative distribution functions. Comptes rendus de l’Académie bulgare des Sciences, 68 (12), 1475-1482.
Kyurkchiev, N. (2016a). Mathematical Concepts in In-surance and Reinsurance. Some Moduli in Programming Environment MATHEMATICA. LAP LAMBERT Academic Publishing, Saarbrucken, 136 pp.
Kyurkchiev, N. (2016b). A family of recurrence gener-ated sigmoidal functions based on the Verhulst logistic function. Some approximation and modelling aspects. Biomath Communications, 3 (2), 18 pp. doi:10.11145/bmc.2016.12.171
Kyurkchiev, N. & Iliev, A. (2016). On the Hausdorff distance between the shifted Heaviside function and some generic growth functions. International Journal of Engi-neering Works, 3 (10), 73-77.
Kyurkchiev, N. & Markov S. (2016b). On the Hausdorff distance between the Heaviside step function and Verhulst logistic function. Journal of Mathematical Chemistry, 54 (1), 109-119. doi:10.1007/S10910-015-0552-0
Kyurkchiev, N. & Markov, S. (2014). Sigmoidal func-tions: some computational and modelling aspects. Biomath Communications, 1 (2), 30-48. doi:10.11145/j.bmc.2015.03.081
Kyurkchiev, N. & Markov, S. (2015). Sigmoid Func-tions: Some Approximation and Modelling Aspects. Some Moduli in Programming Environment Mathematica. LAP LAMBERT Academic Publishing, Saarbrucken.
Kyurkchiev, N. & Markov, S. (2016a). On the numerical solution of the general kinetic K-angle reaction system. Journal of Mathematical Chemistry, 54 (3), 792-805. doi:10.1007/s10910-016-0592-0
Kyurkchiev, N. & Markov, S. (2016c). Hausdorff ap-proximation of the sign function by a class of parametric activation functions. Biomath Communications, 3 (2), 11 pp.
Kyurkchiev, V. & Kyurkchiev N. (2017). A family of recurrence generated functions based on the ”half-hyperbolic tangent activation function”. Biomedical Statis-tics and Informatics, 2 (3). doi:10.11648/j.bsi.20170203.12
Kyurkchiev, V. & Kyurkchiev, N. (2015). On the Ap-proximation of the Step function by Raised-Cosine and Laplace Cumulative Distribution Functions. European International Journal of Science and Technology, 4 (9), 75–84.
Lente, G. (2015). Deterministic Kinetics in Chemistry and Systems Biology. Springer, New York.
Sendov, B. (1990). Hausdorff Approximations. Kluwer, Boston. doi:10.1007/978-94-009-0673-0
