Variation of symmetrical features in the leaf plate of small-leaved lime tree
Variation of symmetrical features in the leaf plate of small-leaved lime tree
Abstract
Fluctuating asymmetry (FA) is a measure of ontogenetic noise indicating a deviation in homeostasis mechanisms. Is the integral value of FA related to the correlation of this index in several traits? A regression model of the integral FA index of the leaf plate of small-leaved lime tree (Tilia cordata Mill) was proposed, which included the following factors:
a) correlation coefficient of the values of the measured leaf plate traits;
b) coefficient of variation of the sizes of these traits;
c) FA correlation coefficient of the traits.
The highest partial regression coefficient was possessed by the variation of traits (b=0.52; p=0.001). The FA correlation coefficient had less significance (b=0.37; p=0.01). The trait correlation factor showed no statistical significant effect on FA value. The method of support vectors confirmed the results of regression analysis and showed the highest predicted FA value at average values of variation of signs and high correlation of signs by FA index.
1. Введение
Симметричные билатеральные структуры в листовой пластине обладают различной флуктуационной изменчивостью. В одних случаях они высоко коррелированы, в других – обладают слабой корреляционной связью по величине флуктуирующей асимметрии (ФА). Пластическая изменчивость (вариабильность величины признаков) – это другой вид фенотипической изменчивости. Изучение двух видов изменчивости показало, что флуктуационная изменчивость скорее положительно коррелировала с вариацией признаков. Для растений такая зависимость зависела от фототаксических особенностей экологических групп древесных растений. В генетическом аспекте предполагается две теоретические схемы расхождения в величине ФА. Первая – независимое проявление с отсутствием корреляции между ФА признаков. Второе – зависимое проявление, т.е. корреляционная связь, которая может быть как положительной, так и отрицательной. Положительная корреляция встречается в половинах листовой пластины даже в отсутствии направленной асимметрии, например, у липы мелколистной. Естественно предположить, что в растениях за ФА отвечает один локус в отдельно взятом гене. Плейотропность здесь проявляется как функция гена, влияющего на многие или все билатерально симметричные признаки, например жилки разных порядков. В то же время полимерия – множественное действие генов на один признак – удобно объясняет отрицательную корреляцию при рассогласованности функционирования генов.
По мнению Sato et al , пластическая изменчивость имеет скорее средовое происхождение, в отличие от шума онтогенетического развития, как генотипического свойства. Известно выражение “plasticity – first” (пластичность – первое). Например, увеличение реакции фитотаксиса (генетическое свойство) ведет к статистически значимой направленной асимметрии, как правило, снижающей долю ФА в билатеральных признаках. В свою очередь, теоретически, это означает повышение стабильности развития или снижение шума развития. Генетические и негенетические аспекты фенотипической изменчивости (флуктуационной и пластической) описаны подробно; общий итог – позитивная корреляция между пластической изменчивостью и шумом развития и обратная связь между шумом развития и флуктуационной изменчивостью ,
, , .Сказанное выше скорее относится к древесным растениям теневыносливого ряда: дуб, черёмуха и липа. Предмет предлагаемого исследования – особенности корреляции признаков в листовой пластине, а также связь между усредненной величиной ФА и коэффициентом корреляции ФА признаков. Разобщенность (слабая корреляция) или согласованность между коэффициентами корреляции (высокая корреляция) может косвенно выражать их генетическую разобщенность.
Целью работы было определение влияния на интегральное значение ФА факторов коэффициента вариации величин признаков и коэффициент вариации значений ФА этих признаков. Дополнительным фактором служил коэффициент корреляция мерных значений признаков. Проверялась следующая гипотеза: вариация (изменчивость) билатерально симметричных признаков и их ковариационная связь по величине флуктуирующей асимметрии оказывает влияние на общую флуктуирующую асимметрию листовой пластины. Как следует из предыдущих исследований, метод геометрической морфометрии, основанный на дисперсии координат меток не всегда отражает результаты, полученные с помощью мерных признаков , . Учитывая это, мы посчитали важным обратить внимание на структуру ФА мерных признаков. Основным методом было моделирование на основе множественной регрессии, дополнительно использовались методы получения данных с помощью системы искусственного интеллекта. Был выбран центральная часть ареала липы мелколистной, листовая пластина которой удобна для исследования, так как обладает достаточно большим числом билатерально-симметричных признаков.
2. Методы и принципы исследования
В работе использовались гербарные материалы, полученные в 2014–2023гг в г. Москва (Измайловский район), Орехово-Зуево и Можайск, а также популяции из Владимирской области. Предыдущие исследования показали ответную реакцию на загрязнения только по некоторым признакам, таким как расстояние, между основаниями первой и второй жилок первого порядка и ширина половины листа, поэтому, важно было оценить популяции по интегрированному показателю.
Листья липы мелколистной собирались в августе-сентябре годов с нижних частей крон, равномерно со всех сторон по 10 листовых пластин с каждого из десяти деревьев по официальной методике с дополнениями , . Места сбора листьев находились как в индустриальных локалитетах, так и в биотопах свободных от антропогенного стресса. После сканирования (300 dpi) изображения листьев двукратно измерялись с помощью экранного дигитайзера TPSdig2 (Rholf, 2017). Результаты измерений мерных признаков сначала заносились в таблицы Excel, затем – в таблицы STATISTICA 10 (Statsoft Ink.), где выполнялись основные анализы описательной статистики. В работе использовались только мерные признаки, угловой признак был исключен (рис. 1).

Рисунок 1 - Признаки для определения ФА
Для нахождения степени вариации признаков (CVприз, пластическая изменчивость) использовался коэффициент вариации как отношение среднеквадратичного отклонения к среднему значению (L+R)/2. Определялся коэффициент корреляции значений ФА от 4-х до 6-ти мерных признаков для каждой популяции. Использовался метод Спирмена, т.к. большинство выборок (L–R)/(L+R), около 8%, обладало непараметрическим распределением.
Проводился регрессионный анализ влияния на ФА коэффициента вариации признаков и коэффициента корреляции между признаками.
Для определения коэффициента корреляции размеров признаков, как и их значений ФА, использовалось взвешенное значение исходя из общего числа признаков. Использовались только статистически значимые коэффициенты, как положительные, так и отрицательные. Везде применялась статистическая значимость α = 95%. Таким образом, каждому популяционному индексу ФА соответствовал:
а) индекс корреляции этого индекса между признаками;
б) коэффициент вариации признаков (CV);
в) коэффициент корреляции между величинами признаков.
Метод опорных факторов (опция Data mining, support vector machine) использовался для прогнозирования. Использовалось 75% объема выборок с 1000 повторностями. Применялось 15 опорных векторов. Обучение проводилось в режиме до 1000 итераций (повторов) до достижения ошибки 0,001 с общим объёмом памяти 40Мб. Формировался объем прогностических значений ФА, находилась корреляция с исходными данными и зависимость между тремя факторами и прогнозируемой величиной флуктуирующей асимметрии.
3. Основные результаты
3.1. Многофакторный регрессионный анализ
Регрессионная модель была статистически значима (F=8,83; р = 0,001), а коэффициент детерминации был равен R2 = 0,58. Остатки, т.е. необъясненные компоненты регрессии были также значимы. Статистически значимыми были 2 фактора: CVприз. (b=0,52; р=0,001) и Rфа (b=0,38; р=0,01, см. табл.1). Отношение дисперсии CVприз. к дисперсии отклика (эта) η2 =0,36. Парциальная корреляция у обоих влияющих фактора была одинакова R2 = 0,15.
Таблица 1 - Факторы регрессии, объясняющие вариацию флуктуирующей асимметрии
Индексы | b* | std.err. | b | std.err. | t(27) | p-value |
CVприз | 0,52 | 0,141 | 0,006 | 0,002 | 3,718 | 0,001 |
Rприз | – 0,02 | 0,137 | – 0,001 | 0,010 | – 0,139 | 0,890 |
Rфа | 0,37 | 0,141 | 0,147 | 0,055 | 2,656 | 0,013 |
Примечание: b* – стандартизированный коэффициент регрессии; b – частный коэффициент регрессии; std.err. – стандартная ошибка; t(27) – критерий Стьюдента; p-value – уровень вероятности
3.2. Метод опорных векторов (Support Vector Machine)
Для прогнозирования результатов регрессии мы использовали автоматическое генерирование множеств данных. Предсказанные значения ФА коррелировали с первоначальными значениями с коэффициентом корреляции равным 0,72. Степень соответствия (goodness of fit) показал соответствие модели для CVприз (r=0,65), и для Rфа (r = 0,55). На рис. 2 показан трехмерный график зависимости предсказанной модели от этих факторов.
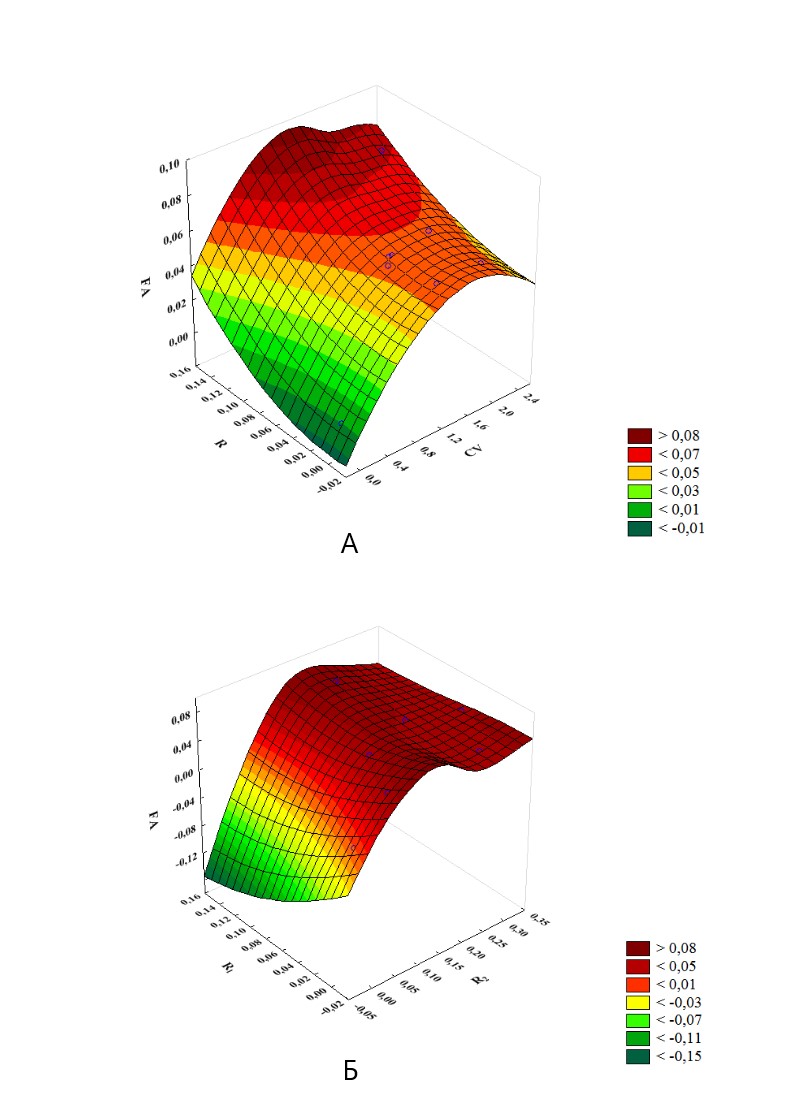
Рисунок 2 - Зависимость предсказанных значений ФА:
А – от коррелированности признаков по ФА (R) и их вариации (CV); Б – от коррелированности признаков по ФА (R1) и корреляции величин признаков (R2)
Третье сочетание факторов CVприз и Rприз показано на рис. 3. Увеличение вариации признаков ведет к увеличению ФА до 0,12 при минимальном значении корреляции между величинами признаков Rприз.
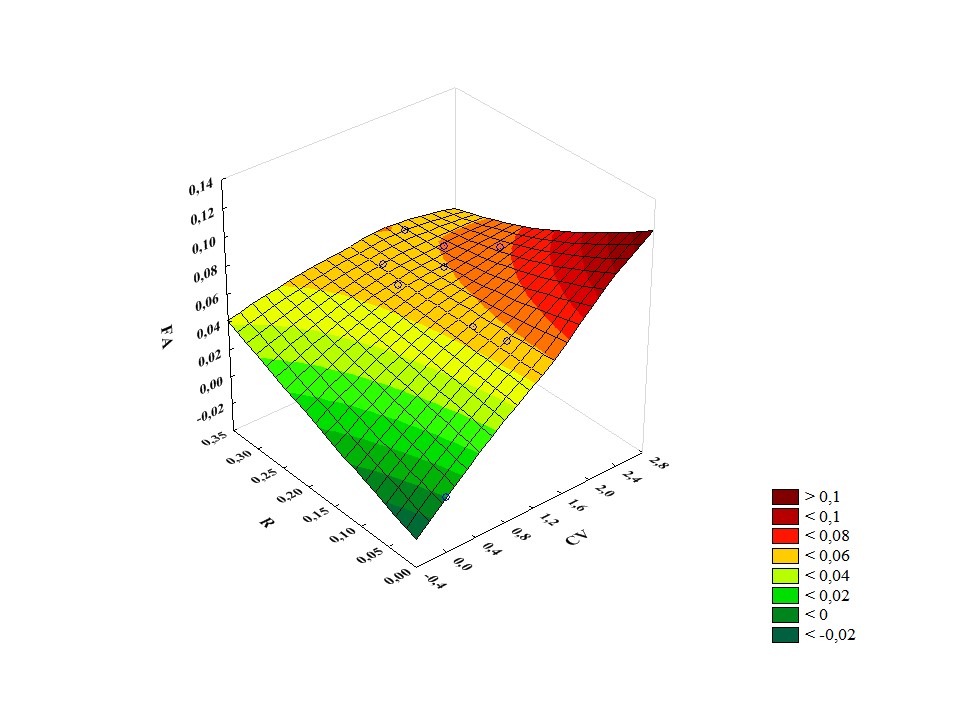
Рисунок 3 - Зависимость предсказанных значений ФА от коррелированности признаков (R) и их вариации (CV)
4. Обсуждение
Выводы, вытекающие из проделаной работы, были следующие:
1. Изменчивость признаков (CV), была наиболее тесно связана с величиной флуктуирующей асимметрии.
2. Все три фактора обладали положительной корреляцией с ФА.
3. Корреляция признаков по величине ФА (низкие значения) в сочетании с высокой вариацией признаков способствовало высокому значению интегральному значению ФА.
Помимо вариации признаков, влияющих на величину ФА , , мы показали, что и корреляция по величине ФА также связана с общей флуктуационной изменчивостью и стабильностью развития.
Гипотеза плейотропного эффекта один ген – множество признаков подтверждалась, т.к., признаки с высокой корреляцией по величине ФА коррелировали с интегральной величиной ФА при среднем и высоком значениях вариации признаков. Этот факт указывает на то, что отклонение от нормы реакции пластических признаков в сторону меньших значений не связано с увеличением ФА и дестабилизацией развития. Высокая флуктуирующая асимметрия при низкой корреляции ФА признаков компенсировалась высокой вариацией самих признаков. Такая связь между пластической и флуктуационной изменчивостью также прослеживается во многих исследованиях ,
, , .5. Заключение
Вызывает интерес адаптивная и неадаптивная виды пластической изменчивости. Другое направление – происхождение шума развития, которое обычно ассоциируют с флуктуационной изменчивостью, как «искажения адаптивной аллометрии» . Модели, по нашему мнению должны включать характеристики распределения случайной величины ,
. Правильный выбор модели имеет важное значение. Например, в нашем случае метод древовидной классификации показал одинаковую значимость обоих факторов: корреляции ФА признаков, и коэффициента вариации признаков. При невысоких объёмах данных рационально использовать множественную регрессию, дополнительная классификация исходных данных требует соответствующих методов.